Standing waves on a one-dimensional string.

Version 0.2, 3-21-07

To do:
(i) Incorporate reflection at boundaries.

Define amplitude, frequency, angular frequency, and wavenumber:

a=0.6,f=m*f_0,w=2*pi*f,l=V/f,k=2*pi/l

Length of string, wavelength and frequency of fundamental mode:

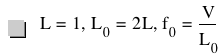
L=1,L_0=2*L,f_0=V/L_0

Speed of wave and harmonic number:

V=slider([0,5,40])

m=slider([1,40,39])

Wave moving to the right:

function(h,x)=a*sin([k*x-(w*n)])

Wave moving to the left:

function(j,x)=a*sin([k*x+w*n])

Sum of wave moving to left and wave moving to right is standing wave:

function(h,x)+function(j,x),0<x<L

function(h,x),0<x<L

function(j,x),0<x<L

d=0.05

abs(y)<d,x<0

abs(y)<d,x>L

Option click on slider play button to get continuous motion in one direction.

Author: David A. Craig <http://web.lemoyne.edu/~craigda/>

Graph of the formula

This file was created by Graphing Calculator 3.5.
Visit Pacific Tech to download the helper application to view and edit these equations live.