You are here: start » whitepapers » narratives » hatom
Using Series of Small White Board Questions to Introduce Students to a New Complex Idea
Physics 426, Monday, March 4, 2013, Day 6
by Novela Auparay, Emily van Zee, Mary Bridget Kustusch, and Corinne A. Manogue
This narrative is based upon a video of the class session and discussions with the instructor, Mary Bridget Kustusch, and the director of the Physics Paradigms Program, Corinne Manogue.
In entering the classroom, each student had picked up a small whiteboard, marker, and cloth to use as an eraser. The students expected that during class the instructor might ask them to write or draw answers to specific questions pertinent to the day’s topic. With some small whiteboard questions, the students merely hold up their whiteboards so the instructor can quickly view their responses and gauge the extent of everyone’s understanding. In this example, however, the instructor collected some of the whiteboards and used them as the focus for an introductory conversation about a topic.
This was the sixth day of Physics 426, Central Forces. The course is divided into two portions, classical and quantum mechanical system. The first 5 days of the course is dedicated to the understanding of the two body problem in the classical systems. One of the goals of the course is to help the upper-division undergrads to perceive the connection of the central forces between the classical and the quantum mechanical systems (for more details of the course see Central Forces).
This narrative presents the first day of the quantum portion of the course. In this lecture, the instructor, Mary Bridget Kustusch, used two different types of small white board questions. First, as an open ended question that led to a rich discussion about the details of the Schrödinger equation. Second, as a staircase of simple prompts that were used to introduce students to a new complex idea. The instructor asked 6 SWBQs in total. Let's discuss the first question of the lecture.
The Schrödinger Equation
As an introduction to the lecture, the instructor compared and contrasted the classical and the quantum systems to get the students to start thinking about the quantum system. After establishing the analogy between Newton's 2nd Law for classical systems and the Schrödinger equation for quantum systems, she asked the students to “Write down the Schrödinger equation.” She gave the class some time to write down their answers as she walked around and skimmed through students' answers. According to MBK, this particular question was intended to ensure that the students understood the importance of the Schrödinger equation and to give them a chance to wrestle with the details and with the differences between bra-ket and wave function notation. With those goals in mind, she chose three different white boards, see figures below.
After showing the boards, the instructor asked, “What do you notice about these?” The open ended nature of this question encouraged the students to converse among themselves before they answered her question. In this example, the instructor listened to the students' conversation and prompted the class when she heard an interesting comment from a student. She then repeated what she heard and started the whole class discussion. This is where the lecturer's ability to respond to students' comments and/or questions might be challenged.
MBK: “So there are 3 things up there and you said they are describing 2 different things. Which is describing which?”
Student A: “The board on the right hand side (refers to Board 3, see Fig.\ref{Board}), … It's just describing the total energy of the system.”
At this point, more students start to comment on the boards. The focus of the class shifted to Board 2 when another student (Student B) said, “ I vote that the middle one is missing something …” Another student (Student E) claimed that the statement on Board 2 is only true when $\hat{H}$ is equal to zero. Instead of correcting it herself, the instructor then asked the class:
MBK: “So, what would I need to change in order to make this a valid statement?”
Student C “Get rid of the …”
Student B: “Take away one of the H hat.”
MBK: “And make it what?”
Student B: “An $i$ and an $h$.”
Student D: “$h$ bar'
MBK: “Which one? this one or this one?” (pointing at each side of the equation.)
Student B: “The right one.” (referring to the right side of the equation.)
After the instructor changed the $\hat{H}$ to $i\hbar$, Student C made a comment that now they had turned Board 2 into Board 1. This comment provoked more students to converse among themselves. In discussing this video, MBK felt that the class had had enough discussion at this point. Most of the students felt comfortable speaking up, filling the class with small conversations. She decided to let control trump the chaos by asking the class to vote on the validity of Board 1.
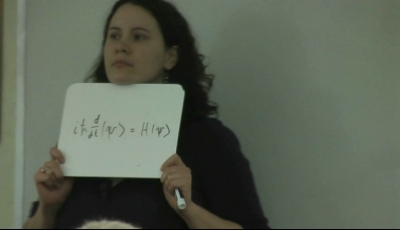 The students spent another minute debating whether the derivative on Board 1 should be a partial or a total derivative. Rather than resolving this debate, MBK chose to start the wrap up discussion about the Schrödinger equation. She used Board 3, which showed the Hamiltonian for a 1D particle-in-a-box, as a bridge to move on to the next part of the lecture which built up the complexity necessary for understanding the quantum central force system.
The students spent another minute debating whether the derivative on Board 1 should be a partial or a total derivative. Rather than resolving this debate, MBK chose to start the wrap up discussion about the Schrödinger equation. She used Board 3, which showed the Hamiltonian for a 1D particle-in-a-box, as a bridge to move on to the next part of the lecture which built up the complexity necessary for understanding the quantum central force system.
Building Up Complexity
To understand the need for a center of mass system to solve the Schrödinger equation of the hydrogen atom, MBK felt the students must first perceive the complexity of the hydrogen system. One way to help them notice this complexity was by using a series of questions that each added another layer of complication.
In this example, the instructor used five different small white board questions to prime a teachable moment. In each case, she gave a prompt and gave the students some time to converse among themselves. For the first question, she took 3 boards from the students, and for every subsequent question, she led a discussion about the prompt without picking up boards.
The instructor's purpose behind any given prompt is crucial in determining the flow of the class discussion. In contrast to the previous SWBQ, this set of questions was not designed to focus on the details of the answers. Rather, the questions were designed to build student understanding of Hamiltonians for different systems. This led to fast-paced discussions compared to the previous discussion. The open ended nature of the question “Write down the Schrödinger equation” led the class to spend more time discussing each question raised by a student compared to the time spent discussing multiple questions raised by students in this series of SWBQs.
Electron in a Uniform Magnetic Field
Prompt:“Talk among yourselves, try to write something down on your white boards, the Hamiltonian of a charged particle, so an electron in a magnetic field in the z direction.”
Though this question is similar to the first prompt: “Write down the Schrödinger equation”, the intention is different. In the interview, the instructor mentioned that she did not aim for same level of detail for the Hamiltonian of this spin particle. The purpose of this question was to build the foundation of the complexity of the hydrogen system and to emphasize that every quantum system has its own Hamiltonian. With that intention in mind, MBK directed the discussion towards making the connection between Board 3 and $\hat{H} = - \vec{\mu} \cdot \vec{B} $. Throughout the discussions about the Hamiltonians for different systems, the instructor kept all six boards (3 boards from the Schrödinger equation question and 3 boards from this question) at the front of the class. She wanted the class to make the connection between these boards themselves.
One Particle in 1-D-Box
MBK started the next portion of the class by re-writing Board 3 on the main board and prompted the students.
Prompt: “OK, what's the momentum operator? Write down on your white boards. (Pause) Now square it. And divide it by 2m.”
A student recognized the answer ($-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}$) as the kinetic energy for the system. The instructor then told the students that this is the Hamiltonian for one particle in a one-dimensional box. Notice that she used a specific series of quick prompts that led the students to the answer. This refers back to the goal of this sequence, not to have detailed discussion, but to help the students make connections between different cases.
Two Particles in 1-D-Box
Prompt: “Write on your white boards what would the Hamiltonian be for two particles in a 1-D-box.”
In this question, MBK did not discuss the students' answers as much. She guided the students by asking direct questions instead of waiting for the students to come up with the questions. For example:
MBK: “OK, we have two particles. Let's think classically, what does the Hamiltonian represent?”
Student E: “Total Energy.”
MBK: “Energy, we have a system of two particles where's the energy come from?”
MBK: “One and two so we have kinetic and potential energy, what is the kinetic energy of particle one?” (Student E points at the board towards the expression of the kinetic energy)
MBK: “Yeah, so we have p one squared over 2m one. OK. We don't have to necessarily have the same mass. What's the kinetic energy of particle two? (Pause) Same thing but twos. OK, Am I done?”
Student E: “No.”
MB: “What else do I need? …”
This fast-paced discussion pattern continued until right before the main discussion at the end of the class.
One Particle in 3-D-Box
Prompt:“So notice we did all these in one dimension. So this really should be p one in the x. Now, write down the Hamiltonian for one particle in 3 dimensions”
The discussion for this question was not long. Most of the students recognized that they needed second order partial derivatives. MBK: “OK, so you're saying this should be U of x, y, z.”
Student F: “First of all those should be squared.”
MBK: “So these should all be squared, OK.”
Student F: “And second of all, there is a nicer way to write all these.”
MBK: “OK so, a nicer way to write all these.”
MBK: “OK first of all before we think about the nicer way to write all these, what do you think about this? U of x, y, z.”
Student F: “Sure.”
The instructor then rewrote the equation from $$\hat{H} = -\frac{\hbar^2}{2m}\left(\frac{\partial^2}{\partial x^2}+ \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2}\right)+ U(x,y,z)$$
to
$$\hat{H}=-\frac{\hbar^2}{2m}\nabla^2+U(x,y,z).$$
Two Particles in 3D-Box
Prompt: “So, we've done 2 particles in 1D, 1 particle in 3D, you can write it in this simple notation. Do 2 particles in 3D.”
In this final question, the instructor did not pick up different boards as she had in the first two SWBQ questions (the Schrödinger equation and the electron in a magnetic field). Rather, she asked the class for a volunteer to write his/her answer on the main board. Student E wrote $\hat{H}=-\frac{\hbar^2}{2}\left(\frac{\nabla_1^2}{m_1}+\frac{\nabla_2^2}{m_2}+U(\vec{r})\right)$. The instructor then spent the last 10 minutes of the class connecting the ideas pulled from students' answers.
Notice that at the end of this sequence of SWBQs, the instructor has become more influential in the discussions and the conversations are mostly between a single student and the instructor. At this point, the students have all the pieces of information that they need. Now it is time for the instructor to tie those pieces together and tell the whole story. In the interview, MBK mentioned that when she wanted to tell the whole story she tended to pick up on the loudest voice in the class to help her advance the conversation. This explains why the conversation was dominated by one student and the instructor.
Another important matter to consider when using SWBQs is not only the intent of asking the questions, but also when not to use the method. SWBQs are useful in reminding students about pieces they already know. Towards the end of the class, the instructor decided not to ask anymore SWBQs, but instead to do an interactive lecture to wrap-up the class discussion. In discussing this video, MBK noted that at this point, it was her role as an instructor to “tell the whole story” and used the various feedback she had received to do that. She did not want to go into great detail like she had when addressing the Schrödinger equation because she did not want the students drawn into mathematical details and to miss the main idea behind the discussions.
Conclusion
In conclusion, we looked at two different uses of SWBQs. First, an open ended question that led to a rich discussion about the details of the Schrödinger equation. Students' answers to the Schrödinger equation persuaded the class to talk about the different representations of the equation, the difference between the energy eigenvalue equation and the Schrödinger equation, and other important details. Notice that the instructor's ability to be responsive to students' comments encouraged many students to be involved in the whole class discussion. Though this is not the main goal of the class, this rich discussion is an astonishing affordance of using SWBQs as an active engagement tool. Notice also that this rich discussion comes from the engagement of the students as well as the responsiveness of the instructor.
Second, we looked at a staircase of simple prompts that were used to introduce students to a new complex idea. The instructor's decisions about when to use and not use SWBQs created the flow of the concepts in the lecture. Observing this quick progression and the flow of the second half of the class helped NA to see the big picture. Seeing how SWBQs helped to make these connections is what encouraged her to write this paper. 
