Homework for Static Fields
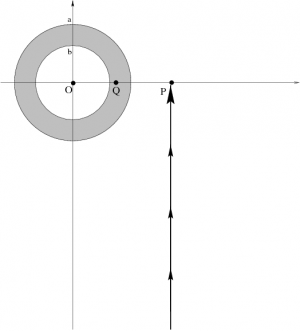
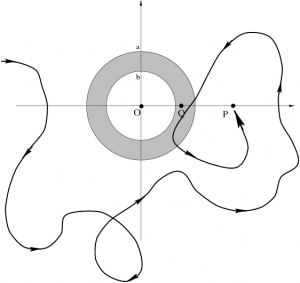
- (PathIndependence) Students explicitly compute the work required to bring a charge from infinity using two different paths. Include part (e) as an additional path that cannot be solved by integration. (You must invoke path-independence of conservative fields.)
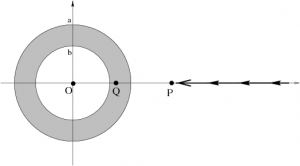
The gravitational field due to a spherical shell of mass is given by: %/* \[ \Vec g =\begin{cases}
0&r<b\\
-\frac{4}{3}\pi\rho\,G\left({r}-{b^3\over r^2}\right)\hat{r}&b<r<a\\ -\frac{4}{3}\pi\rho\, G\left({a^3-b^3\over r^2}\right)\hat{r}&a<r\\
\end{cases}\]
where $b$ is the inside radius of the shell, $a$ is the outside radius of the shell, and $\rho$ is the constant mass density.
Using an explicit line integral, calculate the work required to bring the test mass along the same path, from infinity to the point $Q$ a distance $d$ (where $b<d<a$) from the center of the shell.
Using an explicit line integral, calculate the work required to bring the test mass along the same radial path from infinity all the way to the center of the shell.