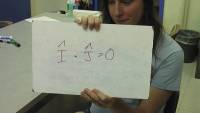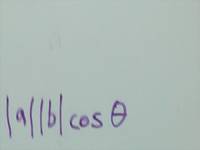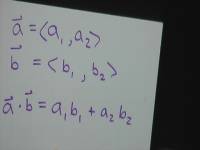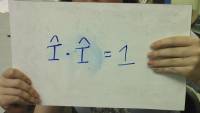You are here: start » swbq » vcsw » vfswdotdef
Recall The Dot Product
The Prompt
“Write down something you know about the dot product.”
Context
This SWBQ opens up discussion about the geometrical meaning of the dot product and the different ways one is likely to see the dot product notated.
Wrap Up
Answers you're likely to see:
Walk around the room as students are answering this question and quickly pick up an example of each different representation or statement. Quickly order them in the order you would like to talk about them and prop them on the chalkboard tray. Pick up each one (or more than one if you are comparing them) and give whatever review “lecture” you would normally give. The students are far more invested if they see that you are talking about their answers and some students will even vie with each other to get you to choose their answer. You can add in any extra representations that the students haven't mentioned as you go along.
The most important thing to emphasize is that the professional physicist knows and uses all of these representations/facts.
You may also want to assign the following homework problem which requires students to use both the algebraic and geometric definitions of the dot product to solve the problem successfully.
- (Tetrahedron)
Using a dot product, find the angle between any two line segments that join the center of a regular tetrahedron to its vertices. Hint: Think of the vertices of the tetrahedron as sitting at the vertices of a cube (at coordinates (0,0,0), (1,1,0), (1,0,1) and (0,1,1)—you may need to build a model and play with it to see how this works!)
Class Video
Powerpoint slide
PDF slide