Homework for Static Fields

  1. (Stokes) Long problem where to verify Stokes' Theorem by comparing the flux of the curl of the magnetic field for a cylindrical wire with the closed line integral of the magnetic field around a loop. Ampere's Law is required to solve several sections of this problem.

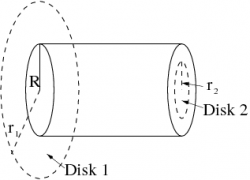
    In this problem, you will be investigating, from several different points of view, a cylindrical wire of finite thickness $R$, carrying a non-uniform current density $J=\kappa s$, where $\kappa$ is a constant and $s$ is the distance from the axis of the cylinder.\\

    1. Find the total current flowing through the wire.\\

    2. Find the current flowing through Disk 2, a central (circular cross-section) portion of the wire out to a radius $r_2<R$.\\

      Figure: cross section of wire

    3. Use Ampère's law in integral form to find the magnetic field at a distance $r_1$ outside the wire.\\

    4. Use Ampère's law in integral form to find the magnetic field at a distance $r_2$ inside the wire.\\

    5. Use theta functions to write the magnetic field everywhere (both inside and outside of the wire) as a single function.\\

    6. Evaluate $$\int \left(\grad\times\BB\right)\cdot d\AA$$ for Disk 2, a circular disk of radius $r_2<R$. Use this result and part (d) to verify Stokes' theorem on this surface.\\

    7. Evaluate $$\int \left(\grad\times\BB\right)\cdot d\AA$$ for Disk 1, a circular disk of radius $r_1>R$. Use this result and part c) to verify Stokes' theorem on this surface.\\


Go Back to the Static Fields Course Content Page
Go Back to the old (3-week) Static Fields Course Content Page


Personal Tools