The Poincaré Disk model of hyperbolic geometry is obtained from the hyperboloid by stereographic projection. Stereographic projection of an ordinary sphere maps the sphere to the $xy$-plane by projecting from the South Pole; points in the Northern Hemisphere ($z>0$) map to the interior of a disk, points in the Southern Hemisphere ($z<0$) map to its exterior, and the Equator ($z=0$) maps to the circle bounding the disk.
The idea of stereographic projection is the same for our Minkowskian hyperboloid. But what are the Poles? As before, they are the two points where the $t$-axis intersects the hyperboloid, but now we need both branches. So the South Pole is the point \begin{equation} P = (0,0,-\rho) \end{equation} (just as for the sphere) and stereographic projection maps each point on the ($t>0$ branch of the) hyperboloid to the interior of a disk in the $xy$-plane.
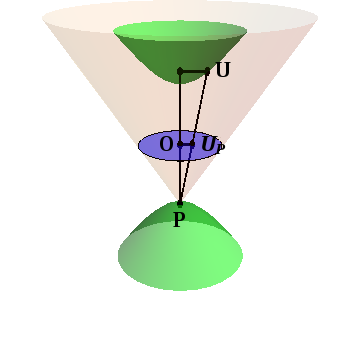 Figure 14.3: Stereographic projection of the hyperboloid.
Figure 14.3: Stereographic projection of the hyperboloid.
Stereographic projection is shown in Figure 14.3, which shows a triangle in a vertical slice through the $t$-axis, taken for simplicity to be in the $xt$-plane. The coordinates of the point $U$ are then \begin{equation} U = (\rho\,\sinh\beta,0,\rho\,\cosh\beta) \end{equation} and the use of similar triangles tells us that the image point $U_P$ has coordinates \begin{equation} U_P = \left(\frac{\rho\,\sinh\beta}{1+\cosh\beta},0,0\right) \end{equation} The image of the general point $U$, with coordinates given by (Equation (4) of §14.2) would be \begin{equation} U_P = (R\,\cos\phi,R\,\sin\phi,0) \end{equation} where \begin{equation} R = \frac{\rho\,\sinh\beta}{1+\cosh\beta} \end{equation} is the radial coordinate in the Poincaré disk. It is now a straightforward exercise in algebra to verify that the line element on the hyperboloid, rewritten in terms of $R$, is just \begin{equation} ds^2 = \frac{4\,\rho^4 \left( dR^2 + R^2\,d\phi^2 \right)}{(\rho^2-R^2)^2} \end{equation} in agreement with the literature for the line element of the Poincaré Disk (which normally assumes $\rho=1$).
We have therefore shown by direct computation that the Poincareé Disk model can be thought of as a relabeling of the points on the hyperboloid; these models are completely equivalent. The Poincaré Disk has the twin advantages of living in two dimensions and not requiring Minkowski space for its construction, but the hyperboloid has the advantage of sharing many obvious symmetries with the sphere.
But what is the Poincaré Disk model? As before, a geometric model is specified by giving its points and lines. Points are points, namely the interior of the unit disk in the $xy$-plane. But what are the lines? Since the lines on the hyperboloid are contained in planes through the origin, but stereographic projection uses lines form the South Pole, the answer to this question is not immediately obvious. It turns out that lines in the Poincaré Disk model are arcs of Euclidean circles that intersect the unit disk orthogonally (at both points of intersection). A special case is of course radial lines, corresponding to circles of infinite radius. Some hyperbolic lines are shown in Figure 14.4,
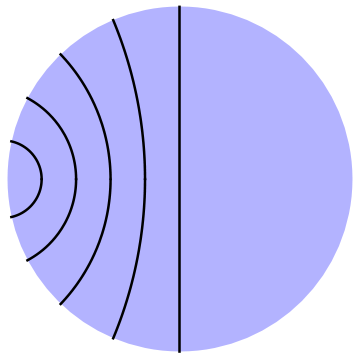 Figure 14.4: Some hyperbolic lines in the Poincaré disk.
Figure 14.4: Some hyperbolic lines in the Poincaré disk.
A closely related model is the Poincaré Half-Plane, which is obtained from the Poincaré Disk using a complex fractional linear transformation, namely \begin{equation} X + iY = 2\frac{i(x+iy)+\rho}{(x+iy)+\rho\,i} \end{equation} where $x+iy=Re^{i\phi}$. Another exercise in algebra verifies that this maps the unit disk onto the half-plane $y\ge0$, and further that \begin{equation} ds^2 = \frac{4\,\rho^4\left(dx^2+dy^2\right)}{(1-x^2-y^2)^2} = \rho^2\>\frac{dX^2+dY^2}{Y^2} \end{equation} (where $x^2+y^2=R^2$), which again agrees with the literature (for $\rho=1$).
The points in the Poincaré Half-Plane model of hyperbolic geometry are the points in the $xy$-plane with $y>0$, and the lines are (open, Euclidean) semicircles of any radius centered at points along the $x$-axis, including vertical lines, which correspond to infinite (Euclidean) radius.
Both the Poincaré Disk and Poincaré Half-Plane models are conformal models, in that they are multiples of the ordinary Euclidean metric. Since all distances are merely rescaled, angles can be defined through the dot product are unaffected by the rescaling, which cancels out. Thus, angles in both of these models can be measured with Euclidean protractors.