Special relativity is about inertial observers, moving at constant velocity. Consider now an observer undergoing uniform acceleration. What does this mean?

We start with Newton's Second Law in the form \begin{equation} F = \frac{dp}{dt} = ma \end{equation} but we use the relativistic notion of momentum, so that \begin{equation} p = mc\,\sinh\beta \end{equation} Setting $a=\hbox{constant}$ is equivalent to assuming that $p$ is a linear function of $t$, leading to \begin{equation} \sinh\beta = \frac{at}{c} \end{equation} But we also have \begin{equation} v = \frac{dx}{dt} = c\,\tanh\beta \end{equation} so that \begin{equation} dx = \frac{c^2}{a}\,\sinh\beta\,d\beta \end{equation} and it is easy to solve this differential equation for $x$.

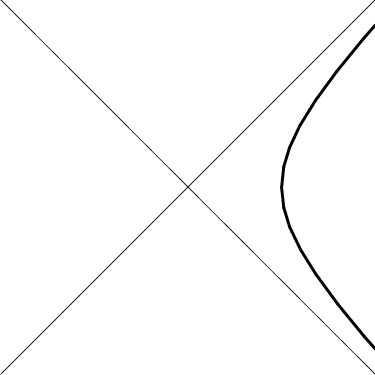Figure 13.6: The trajectory of a uniformly accelerating object.

Trajectories of uniform acceleration are therefore given by \begin{eqnarray} x &=& \frac{c^2}{a} \,\cosh\beta \\ t &=& \frac{c}{a} \,\sinh\beta \end{eqnarray} In other words, uniform acceleration corresponds to worldlines which are hyperbolas, as shown in Figure 13.6. These hyperbolas are just our old friends, “circles” of constant distance from the origin! We now discuss the physical implications of their geometric properties.

First of all, the instantaneous speed of the accelerating object is given by the (inverse) slope of the worldline at that point. A hyperbolic worldline describes an object which is instantaneously at rest at $t=0$, but whose speed approaches the speed of light as $t$ goes to $\infty$. No, you can't actually travel at the speed of light, but with uniform acceleration you can come arbitrarily close.

The asymptotes of our hyperbolic worldline are lines at $45^\circ$, and could therefore represent beams of light. This means that an object undergoing uniform acceleration can outrun a light beam! All that is necessary is to have a head start — and to end the race after finite time.

Furthermore, the region of spacetime behind that light beam is invisible to the uniformly accelerating object. More precisely, no signal originating at $x<0$ when $t=0$ can ever reach the object. No light can escape this region. This is precisely the geometric idea behind black holes!

The geometry shown in Figure 13.6 is in fact very similar to that of the Schwarzschild black hole. “Stationary” observers far away remain at constant distance from the black hole, despite the gravitational field; they are therefore undergoing uniform acceleration equal and opposite to that of gravity. There is a region of spacetime “inside” the black hole, from which a light beam can never escape. Both of these properties are correctly modeled by our much simpler model involving uniform acceleration but no gravity.