1. The mast of a sailboat leans at an angle $\theta$ (measured from the deck) towards the rear of the boat. An observer on the dock sees the boat go by at speed $v\ll c$ (so that you do not need to use relativity to do this problem). What angle does the observer say the mast makes?
2. A child on the boat throws a ball into the air at the same angle $\theta$. What angle does the observer on the dock say the ball makes with the deck? (Ignore the subsequent influence of gravity on the ball — this question is only about the initial angle when the ball leaves the child's hand.)
3. A spaceship goes past the dock at speed $v$. An antenna is mounted on the hull at an angle $\theta$ with the (horizontal) hull. What angle does the observer on the dock say the antenna makes?
4. A spotlight is mounted on the spaceship so that its beam makes an angle $\theta$ with the hull. What angle does the observer on the dock say the beam makes with the hull?

 
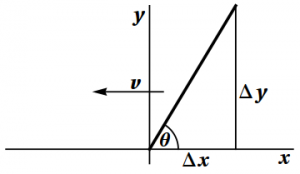
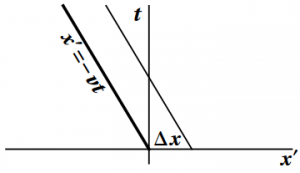
Figure 7.6: The angle made by the mast of a moving sailboat. The figure on the left shows the angle made by the mast, while the figure on the right shows the speed of the mast. (Primed coordinates refer to the dock.)

1. See Figure 7.6. The angles are the same, since both observers agree on the lengths of the sides of the right triangle made by the mast and the deck. Using primed coordinates to refer to the dock, and unprimed coordinates for the sailboat, we have \begin{eqnarray} \Delta x' &=& \Delta x \\ \Delta y' &=& \Delta y \end{eqnarray} so that \begin{equation} \tan\theta' = \frac{\Delta y'}{\Delta x'} = \frac{\Delta y}{\Delta x} = \tan\theta \end{equation}

 
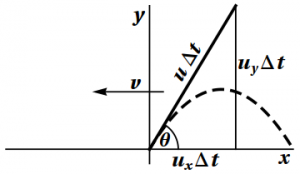
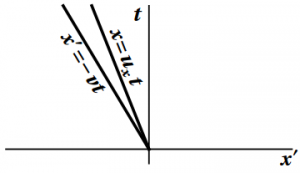
Figure 7.7: The angle made by a ball thrown from a moving sailboat. The figure on the left shows the angle made by the ball, while the figure on the right shows the speed of the ball.

2. See Figure 7.7. The right triangle used to determine this angle now involves velocities, not lengths, and velocities are different as measured by the two observers. We have \begin{eqnarray} u_x' &=& u_x - v \\ u_y' &=& u_y \end{eqnarray} so that \begin{equation} \tan\theta' = \frac{u_y'}{u_x'} = \frac{u_y}{u_x-v} = \frac{\tan\theta}{1-\frac{v}{u\cos\theta}} = \frac{u\sin\theta}{u\cos\theta-v} \end{equation}

 
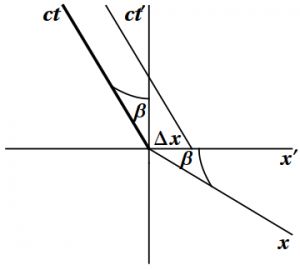
Figure 7.8: The angle made by an antenna on a moving spaceship. The figure on the left shows the angle made by the antenna, while the figure on the right shows the Lorentz transformation between frames.

3. See Figure 7.8. Now we have to take length contraction into account. We have \begin{eqnarray} \Delta x' &=& \frac{\Delta x}{\cosh\beta} \\ \Delta y' &=& \Delta y \end{eqnarray} so that \begin{equation} \tan\theta' = \frac{\Delta y'}{\Delta x'} = \frac{\Delta y}{\Delta x}\cosh\beta = \tan\theta\cosh\beta > \tan\theta \end{equation}

 
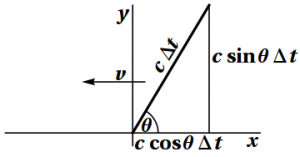
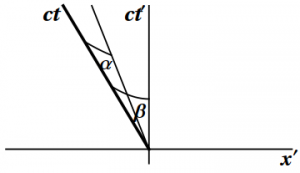
Figure 7.9: The angle made by the beam of a moving searchlight. The figure on the left shows the (Euclidean) angle made by the beam, while the figure on the right shows the (hyperbolic) angle between the two reference frames.

4. See Figure 7.9. We must now deal both with the hyperbolic angle due to the spaceship's velocity and the Euclidean angle formed by the beam of light, which does not travel at the speed of light in the direction of the spaceship. We have as usual $\frac{v}{c}=\tanh\beta$, where $v$ is the speed of the spaceship. The component of the velocity of the beam of light in this direction is given by \begin{equation} \tanh\alpha = \cos\theta \end{equation} as can be seen using the first diagram in Figure 7.9. Using the second diagram in Figure 7.9, we see that \begin{equation} -\cos\theta' = \tanh(\beta-\alpha) = \frac{\tanh\beta-\tanh\alpha}{1-\tanh\beta\tanh\alpha} = \frac{v-c\cos\theta}{c-v\cos\theta} \end{equation}