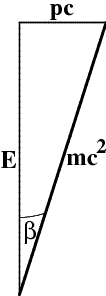- §1. Proper Time
- §2. Energy and Momentum
- §3. Conservation Laws
- §4. Energy
- §5. Useful Formulas
Energy
This mystery is resolved by recalling that momentum is mass times velocity, and that there is also a “$t$-component” to the velocity. In analogy with the 2-velocity, we therefore define the “2-momentum” to be \begin{equation} \bp = m \pmatrix{\cc\frac{dt}{d\tau}\cr \frac{dx}{d\tau}} = m\cc \pmatrix{\cosh\alpha\cr \sinh\alpha\cr} \end{equation} The second term is clearly the momentum, which we denote by $p$, but what is the first term? If the object is at rest, $\alpha=0$, and the first term is therefore just $mc$. But Einstein's famous equation \begin{equation} E=mc^2 \end{equation} leads us to suspect that this is some sort of energy. In fact, $mc^2$ is called the rest energy or rest mass.
In general, we define the energy of an object moving at speed $u=\cc\,\tanh\alpha$ to be the first component of $\bp$, that is we define \begin{eqnarray} E &:=& m \csq \cosh\alpha \label{MomMasterI}\\ \end{eqnarray}\begin{eqnarray} p &:=& m \cc \, \sinh\alpha \label{MomMasterII} \end{eqnarray} or equivalently \begin{equation} \bp = \pmatrix{\cm E\cr p} \end{equation}
Is this definition reasonable? Consider the case $\uc\ll1$. Then \begin{eqnarray} E &=& m\csq\cosh\alpha = m\csq\gamma \nonumber\\ &=& \frac{m\csq}{\sqrt{1-\uucsq}} \\ &\approx& m \csq + \frac12\, m u^2 + \frac38\, m \,\overcc{u^4} + … \nonumber \end{eqnarray} The first term is the rest energy, the next term is the Newtonian kinetic energy, and the remaining terms are relativistic corrections to the kinetic energy.
The moral is that conservation of 2-momentum is equivalent to both conservation of momentum and conservation of energy, but that there is no requirement that the total mass be conserved.
Taking the (squared) norm of the 2-momentum, we obtain \begin{equation} -\csq \bp\cdot\bp = E^2 - p^2\csq = m^2\cfour \label{RestMass} \end{equation} The geometry of this situation is shown in Figure 9.2.
Note that ($\ref{RestMass}$) continues to makes sense if $m=0$, although the expressions for $E$ and $p$ separately in terms of $\alpha$ or $\gamma$ do not. In fact, $\gamma$ must approach $\infty$, or equivalently $\uucsq=1$, so that $|u|=\cc$; such particles always move at the speed of light!
We therefore conclude that there can be massless particles, which move at the speed of light, and which satisfy ($m=0$ and) \begin{equation} E = |p| \cc \ne 0 \end{equation} Photons are examples of such particles; quantum mechanically, one has $E=\hbar\nu$, where $\nu$ is the frequency of the light (and $\hbar=\frac{h}{2\pi}$ where $h$ is Planck's constant).