We now investigate moving clocks. Consider first the smaller dot in Figure 6.3. This corresponds to $\cc t=1$ (and $x=0$), as evidenced by the fact that this point is on the (other) unit hyperbola, as shown. Similarly, the larger dot, lying on the same hyperbola, corresponds to $\cc t'=1$ (and $x'=0$). The horizontal line emanating from this dot gives the value of $\cc t$ there, which is clearly greater than 1, and which represents the time according to the observer at rest when the moving clock says 1. According to the observer at rest, the moving clock therefore runs slow. But now consider the diagonal line emanating from the larger dot. At all points along this line, $\cc t'=1$. In particular, at the smaller dot we must have $\cc t'>1$. Thus, the time according to the moving observer when the clock at rest says 1 (at the smaller dot) must be greater than 1; the moving observer therefore concludes the clock at rest runs slow!
There is no contradiction here; one must simply be careful to ask the right question. In each case, observing a clock in another frame of reference corresponds to a projection. In each case, a clock in relative motion to the observer appears to run slow.
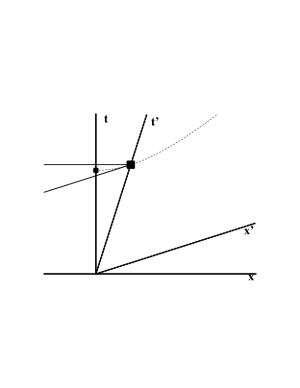 Figure 6.3: Time dilation as a hyperbolic projection.
Figure 6.3: Time dilation as a hyperbolic projection.
To determine the exact value measured by the moving observer, we return to the bouncing beam of light considered in Chapter 2. Figure 2.5 showed the relationships between the various distances, but we would now like to draw a spacetime diagram for this scenario. However, since the beam of light is moving in both the horizontal ($x$) and vertical ($y$) directions, we need a three-dimensional spacetime diagram, as shown in Figure 6.4.
In this diagram, the vertical line represents an observer at rest on the platform, while the mostly vertical line on the right represents the motion of the flashlight on (the floor of) the moving train. The beam of light is the line in the back of the diagram, along the light cone, and moving in both the $x$ and $y$ directions.
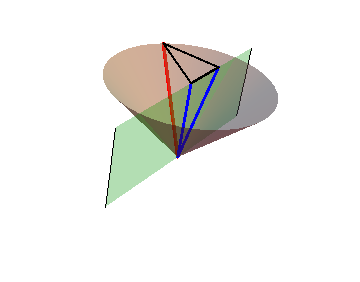
Figure 6.4: The three-dimensional spacetime diagram for a bouncing beam of light on a
moving train. The beam of light is along the light cone, and is projected
both into the $xy$-plane (top) and the $xt$-plane (front).
Projecting this figure into a horizontal plane (with $t=\hbox{constant}$), as shown at the top of the cone, one recovers precisely Figure 2.5: The base of the triangle corresponds to the distance $v\,\Delta t$ traveled by the train, the hypotenuse to the distance $c\,\Delta t$ traveled by the beam of light according to the observer on the platform, and the remaining leg to the height of the train, that is, to the distance $c\,\Delta t'$ traveled by the beam of light according to the observer on the train. % Projecting this figure instead into the vertical plane (with $y=0$), as shown in the middle of the cone, one obtains the spacetime diagram shown in Figure 6.5.
The edges of these two triangles have the same lengths! To see this, note first of all that they share one edge. But each of the remaining pairs of edges form the legs of a right triangle, whose hypotenuse is the beam of light. Since the speed of light is 1 (in appropriate units), in each case the legs must have the same length. This argument justifies the labeling used in Figure 6.5, and can in fact be used to derive the hyperbolic Pythagorean theorem, which says here that \begin{equation} (c\,\Delta t')^2 = (c\,\Delta t)^2 - (v\,\Delta t)^2 \end{equation} or equivalently that \begin{equation} t' = \frac{t}{\cosh\beta} \end{equation} where $\tanh\beta=v/c$ is the speed of the train. Moving clocks therefore run slow, and by a factor of precisely $\cosh\beta$.
It is worth comparing Figures \ref{trainT} and \ref{trainH}, using Figure 6.4 as needed. These two diagrams are almost the same, but two of the edges appear to have been interchanged. In the first diagram, the vertical distance traveled by the beam of light was $c\Delta t'$; in the second, the time taken by the beam to reach the top of the train is $c\Delta t'$ (in appropriate units), namely the length of the (projected) worldline of the beam of light, which is the hypotenuse of the triangle.
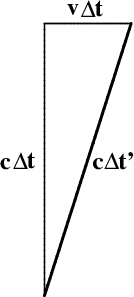
Figure 6.5: The spacetime Pythagorean theorem for a bouncing light beam on a moving
train.