Now consider a new set of coordinates, call them $(x',y')$, based on axes rotated counterclockwise through an angle $\theta$ from the original ones, as shown in Figure 3.5. For instance, the $y$-axis could point towards true north, whereas the $y'$-axis might point towards magnetic north. In the primed coordinate system, the point $B$ has coordinates $(r,0)$, and the point $A$ has coordinates $(0,r)$, while the unprimed coordinates of $B$ and $A$ are $(r\cos\theta,r\sin\theta)$ and $(-r\sin\theta,r\cos\theta)$, respectively. A little work shows that the coordinate systems are related by a rotation matrix \begin{equation} \pmatrix{x\cr y\cr} = \pmatrix{ \cos\theta& \sin\theta\cr -\sin\theta& \cos\theta\cr} \pmatrix{x'\cr y'\cr} \end{equation} (where we are of course assuming that all coordinates are measured in the same units!). Furthermore, both coordinate systems lead to the same result for the (squared) distance, since \begin{equation} x^2 + y^2 = x'^2 + y'^2 \end{equation}
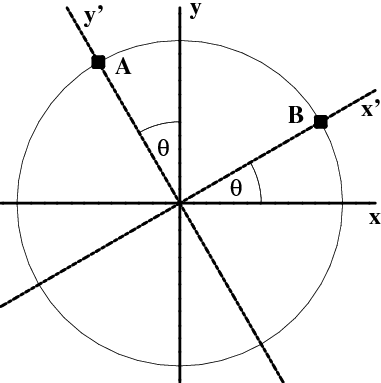 Figure 3.5: A rotated coordinate system.
Figure 3.5: A rotated coordinate system.