- §1. The Surveyors
- §2. Spacetime Diagrams
- §3. Lorentz Transformations
- §4. Space and Time
- §5. Dot Product
Lorentz Transformations
We now relate Lorentz transformations, based on the physical postulates of special relativity, to hyperbola geometry.
The Lorentz transformation between a frame $(x,t)$ at rest and a frame $(x',t')$ moving to the right at speed $v$ was derived in Chapter 2. The transformation from the moving frame to the frame at rest is given by \begin{eqnarray} x &=& \gamma\,(x'+vt') \\ t &=& \gamma \left(t'+\vcsq x'\right) \end{eqnarray} where \begin{equation} \gamma = \frac{1}{\gammainv} \end{equation} The key to converting this to hyperbola geometry is to measure space and time in the same units by replacing $t$ by $ct$. The transformation from the moving frame, which we now denote $(x',\cc t')$, to the frame at rest, now denoted $(x,\cc t)$, is given by \begin{eqnarray} x &=& \gamma \, (x' + \vc\, \cc t') \\ \cc t &=& \gamma \left( \cc t' + \vc\, x' \right) \end{eqnarray} which makes the symmetry between these equations much more obvious.
We can simplify things still further. Introduce the rapidity $\beta$ via 1) \begin{equation} \vc = \tanh\beta \end{equation} Inserting this into the expression for $\gamma$ we obtain \begin{equation} \gamma = \frac{1}{\sqrt{1-\tanh^2\beta}} = \sqrt{\frac{\cosh^2\beta}{\cosh^2\beta-\sinh^2\beta}} = \cosh\beta \end{equation} and \begin{equation} \vc\,\gamma = \tanh\beta\cosh\beta = \sinh\beta \end{equation}
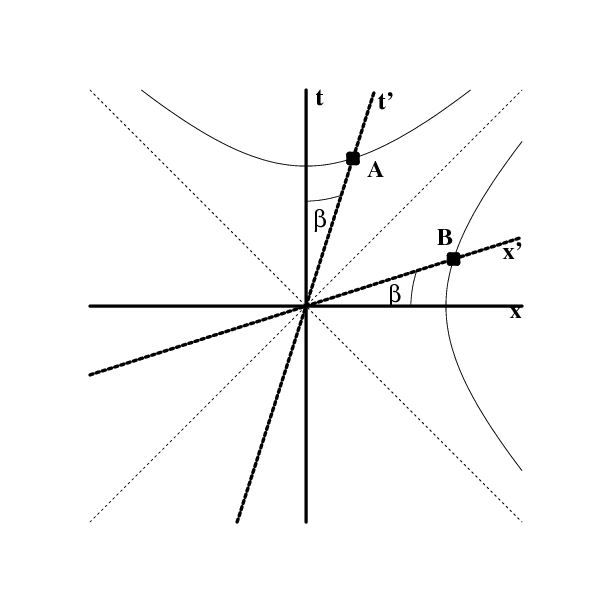 Figure 5.2: The Lorentz transformation between an observer at rest and an observer
moving at speed $\vc=\tanh\beta$ is shown as a hyperbolic rotation.
The point $A$ has coordinates $(\rho\,\sinh\beta,\rho\,\cosh\beta)$, and $B=(\rho\,\cosh\beta,\rho\,\sinh\beta)$. (Units have been chosen such that $c=1$.)
Figure 5.2: The Lorentz transformation between an observer at rest and an observer
moving at speed $\vc=\tanh\beta$ is shown as a hyperbolic rotation.
The point $A$ has coordinates $(\rho\,\sinh\beta,\rho\,\cosh\beta)$, and $B=(\rho\,\cosh\beta,\rho\,\sinh\beta)$. (Units have been chosen such that $c=1$.)
Inserting these identities into the Lorentz transformations above brings them to the remarkably simple form \begin{eqnarray} x &=& x'\cosh\beta + ct'\sinh\beta \\ ct &=& x'\sinh\beta + ct'\cosh\beta \end{eqnarray} which in matrix form is just \begin{equation} \pmatrix{x\cr \cc t} = \pmatrix{\cosh\beta& \sinh\beta\cr \sinh\beta& \cosh\beta\cr} \pmatrix{x'\cr \cc t'} \label{hyperLorentz} \end{equation} But ($\ref{hyperLorentz}$) is just (1) of §4.4. with $y=\cc t$!
Thus, Lorentz transformations are just hyperbolic rotations! As noted in the previous chapter, the invariance of the interval follows immediately from the fundamental hyperbolic trigonometric identity (4) of §4.1. This invariance now takes the form \begin{equation} x^2 - \csq t^2 \equiv x'^2 - \csq t'^2 \end{equation} as shown in Figure 5.2; compare Figure 4.2. The physics of Lorentz transformations and the (Lorentzian) geometry of hyperbolas are therefore one and the same; hyperbola geometry is the geometry of special relativity.