- §1. Cosmology
- §2. Cosmological Principle
- §3. Constant Curvature
- §4. Robertson-Walker Metrics
- §5. The Big Bang
- §6. Friedmann Cosmologies
- §7. FRW Vacuum Models
- §8. Missing Matter
- §9. Standard Models
- §10. Cosmological Redshift
Cosmological Redshift
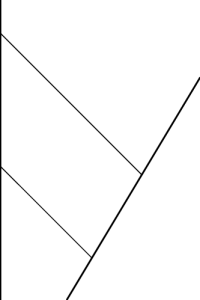
In special relativity, light emitted by a moving observer at one frequency is received by a stationary observer at another frequency. This is the Doppler effect, which can be computed using Figure 1. In this case, the two heavy lines correspond to observers moving at different velocities, and the two lighter lines correspond to pulses of light, emitted by the moving observer (on the right), and received by the stationary observer (on the left). Simple (hyperbolic) triangle trigonometry can be used to compute the ratio of the time intervals between the two pulses as seen by the two observers.
The same diagram can be used to compute the cosmological redshift, but the interpretation is quite different. The two heavy lines now correspond to two observers in the same reference frame; since the universe is expanding, these observers are not at rest with respect to each other. Each of these worldlines can therefore be described by $r=\hbox{constant}$.
Along each light beam, the line element takes the form \begin{equation} 0 = ds^2 = -dt^2 + \frac{a^2\,dr^2}{1-kr^2} = -dt^2 + a^2\,d\psi^2 \end{equation} so that \begin{equation} d\psi = - \frac{dt}{a} \end{equation} where the sign is chosen to imply an incoming light beam from a galaxy far away. This expression can be integrated along each light beam, but the answer must be the same in both cases since $\psi=\hbox{constant}$ along each worldline. If the light beams are emitted close together, the rescaled time differences $dt/a$ between pulses must therefore be the same for both observers, which we write as \begin{equation} \frac{dt_0}{a_0} = \frac{dt_1}{a_1} \end{equation} The ratio of the wavelengths is given by \begin{equation} \frac{\lambda_0}{\lambda_1} = \frac{dt_0}{dt_1} = \frac{a_0}{a_1} \end{equation} and the cosmological redshift $z$ is defined via the ratio of the frequencies, that is \begin{equation} 1+z = \frac{\nu_1}{\nu_0} = \frac{\lambda_0}{\lambda_1} \end{equation} Thus, we have \begin{equation} 1+z = \frac{a(t_0)}{a(t_1)} \end{equation} where $t_0$ (respectively, $t_1$) is the time the (first) light beam is received (respectively, emitted) by the corresponding observer.
Assuming finally that these times are close together, we have \begin{equation} 1 + z = \frac{a(t_1+dt)}{a(t_1)} \approx \frac{a(t_1)+\dot{a}(t_1)\,dt}{a(t_1)} = 1 + \frac{\dot{a}}{a}\bigg|_{t_1} \,dt \end{equation} This is Hubble's Law, which says that the redshift $z$ of a galaxy a distance $d$ away is given approximately by \begin{equation} z \approx \frac{\dot{a}}{a} \>d \end{equation} since the time it takes to receive the light beam is the same as the distance to the object. The (present value of the) “constant” $\dot{a}/a$ is called Hubble's constant.