The Divergence in Curvilinear Coordinates
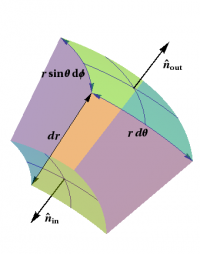 Figure 1: Computing the radial contribution of the flux through a small box in
spherical coordinates.
Figure 1: Computing the radial contribution of the flux through a small box in
spherical coordinates.
The divergence is defined in terms of flux per unit volume. In § {Divergence}, we used this geometric definition to derive an expression for $\grad\cdot\EE$ in rectangular coordinates, namely \begin{eqnarray*} \grad\cdot\EE = \frac{\rm flux}{\rm unit volume} = \Partial{E_x}{x} + \Partial{E_y}{y} + \Partial{E_z}{z} \end{eqnarray*}
Similar computations to those in rectangular coordinates can be done using boxes adapted to other coordinate systems. Not surprisingly, this introduces some additional factors of $r$ (and $\sin\theta$). For instance, consider a radial vector field of the form \begin{eqnarray*} \EE = E_r\,\rhat \end{eqnarray*} where $\rhat$ is the unit vector in the radial direction. The electric field of a point charge would have this form. What is the flux of $\EE$ through a small box around an arbitrary point $P$, whose sides are surfaces with one of the spherical coordinates held constant, as shown in Figure 1? Only the two sides which are parts of spheres contribute, and each such contribution takes the form \begin{eqnarray*} \EE\cdot d\AA = \pm E_r \,r^2\sin\theta\,d\theta\,d\phi \end{eqnarray*} An argument similar to the one used in rectangular coordinates leads to \begin{eqnarray*} \EE\cdot d\AA = \Partial{}{r}\Bigl(r^2 E_r\Bigr) \sin\theta\,dr\,d\theta\,d\phi = \frac{1}{r^2} \Partial{}{r}\Bigl(r^2 E_r\Bigr) \,dV \end{eqnarray*} where it is important to note that the factor of $r^2$ must also be differentiated. It now finally follows that \begin{eqnarray*} \grad\cdot\EE = \frac{1}{r^2} \Partial{}{r}\Bigl(r^2 E_r\Bigr) \end{eqnarray*}
This expression only gives the divergence of the very special vector field $\EE$ given above. The full expression for the divergence in spherical coordinates is obtained by performing a similar analysis of the flux of an arbitrary vector field $\FF$ through our small box; the result can be found § {Formulas for Div, Grad, Curl}. This formula, as well as similar formulas for other vector derivatives in rectangular, cylindrical, and spherical coordinates, are sufficiently important to the study of electromagnetism that they can, for instance, be found on the inside front cover of Griffiths' textbook, Introduction to Electrodynamics.