Curvature measures the rate at which a space curve r(t) changes direction. The direction of curve is given by the unit tangent vector
![]()
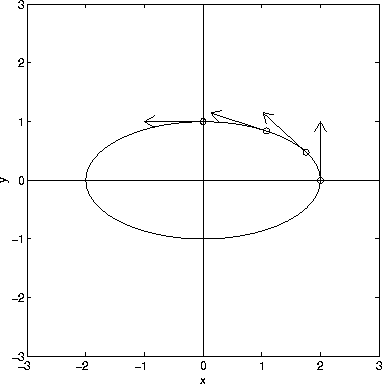
which has length 1 and is tangent to r(t). The picture below shows the unit tangent vector T(t) to the curve r(t)=<2cos(t),sin(t)> at several points.
Obviously, if r(t) is a straight line, the curvature is 0. Otherwise the curvature is non-zero. To be precise, curvature is defined to be the magnitude of the rate of change of the unit vector with respect to arc length:
![]()
The reason that arc length comes into the definition is that arc length is independent of parameterization.
In most cases a curve is described by a particular parameterization and we have the unit tangent vector as a function of t: T(t). We can compute the curvature using the chain rule
![]()
Recall that ds/dt=|r'(t)|. Hence, it follows that
![]()
What is the curvature of the ellipse r(t)=<2cos(t),sin(t)>? We have several computations to perform. First, we have
![]()
and
![]()
implying
![]()
Differentiating again, we have
![]()
Finally, we have
![]()
Look at the graph of the ellipse above. The curvature is greatest near x=2 and y=0 and x=-2 and y=0. These points correspond to t=0 and t=pi. In the above expression for the curvature, the denominator is at its minimum when t=0 or t=pi, implying the curvature is at a maximum. The plot of ellipse indicates that the curvature is at is lowest value when y=1 and x=0 and y=-1 and x=0. These points correspond to t=pi/2 and 3*pi/2. For these values of t the curvature takes on its minimum value in the formula above.
Curvature of a Circle
A circle of radius a can be described by the parameterization r(t)=a<cos(t),sin(t)>. It can be shown that
![]()
and
![]()
implying
![]()
Differentiating again, we have
![]()
Finally, we have
![]()
Alternative formula for the Curvature
It can be shown that the curvature is also given by the formula
![]()
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.