Numerical Methods for Second-Order ODE

Most ordinary differential equations arising in real-world applications
cannot be solved exactly. These ode can be analyized qualitatively.
However, qualitative analysis may not be able to give accurate answers.
A numerical method can be used to get an accurate approximate solution
to a differential equation. There are many programs and packages for
solving differential equations. With today's computer, an accurate
solution can be obtained rapidly. In this section we focus on Euler's
method, a basic numerical method for solving initial value problems.

Consider the differential equation:

The first step is to convert the above second-order ode into two
first-order ode. This is a standard operation. Let v(t)=y'(t).
Then v'(t)=y''(t). We then get two differential equations. The
first is easy

The second is obtained by rewriting the original ode. Using the fact
that y''=v' and y'=v,

The initial conditions are y(0)=1 and y'(0)=v(0)=2.

We are now ready to approximate the two first-order ode by Euler's
method. A derivation of Euler's method is given the numerical methods
section for first-order ode. We first discretize the time interval.
Let 0=t_0. Let t_1<t_2<t_3< ... be other points. We approximate
the solution at these gridpoints. For simplicity we will assume that
the points are equispaced. In general they need not be. Let us define
z_k to be the approximation to y(t) at t_k and let w_k be the
approximation to v(t) at t_k. For our example we get the following
recursion formulas for z_k and w_k:

The initial conditions are z_0=y(0)=1 and w_0=v(0)=2. Here Dt is the
spacing between gridpoints.

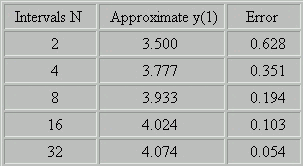
Suppose our goal is to compute the solution to the model differential
equation at time t=1. The exact solution, obtained using an advanced
algorithm, is 4.1278. The following table summarizes the results obtained
using Euler's method. Note that the error decreases as the number
of gridpoints N increases. Here the spacing between points is 1/N.

Summary

Consider the second-order ode:

Suppose the goal is solve the problem on the interval [t_0,T]. The
following list summarizes the steps in solving the problem by Euler'
method.

• Convert the second-order ode into two first-order ode. Let
  v=y'. Then the two odes are

  

  

• Discretize the interval [t_0,T]. Pick a bunch of points
  t_0<t_1<t_2<...<t_N=T. The points need not be equispaced.
• Let z_k denote the approximation to y(t_k) and let w_k denote the
  approximation to v(t_k).
• Use the formulas

  

  

  to compute the approximate solution for k=0,1,2,...
  

Software for Solving Differential Equations Numerically

• Netlib: This is a repository for all sorts of mathematical software.
  Most of the programs are in C or Fortran. Look under ode or odepack.
• Maple, Mathematica, Matlab: These are packages for doing numerical
  and symbolic computations. They have routines for solving ode
  numerically.

[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.