Euler's Method for First-Order ODE

Most ordinary differential equations arising in real-world applications cannot be
solved exactly. These ode can be analyzed qualitatively. However, qualitative
analysis cannot give accurate answers. A numerical method can be used to get
an accurate approximate solution to a differential equation. There are many
programs and packages for solving differential equations. With today's
computers, an accurate solution can be obtained rapidly. In this section we
focus on Euler's method, a basic numerical method for solving differential
equations.

We illustrate Euler's method by considering the differential equation:

This is an example of linear ode and can be solved exactly; the answer is

Suppose our goal is to compute the solution at t=1. We will do this using two steps
of size 0.5. Our goal is to approximate the solution at t_1=0.5 and t_2=1. Let us call
denote v_i to be the approximate solution at t_i. We let 0=t_0 and y(0)=1=v_0.

We proceed by first determining v_1. According to the differential equation, the
slope at t_0 is y'=f(t_0,v_0). If we assume that the slope is constant between
t_0 and t_1, then we get the following approximation for v_1

where h=t_1-t_0 is the stepsize. For the model problem we have

The figure below shows how the approximation compares to the exact solution.
Remember, v_1 is obtained by assuming that the initial slope f(t_0,v_0) is
constant in the time interval. Since the slope of the exact solution f(t,y)=t+y
is increasing as t increases, our approximation v_1=1.5 is less than the exact
answer y(t_1)=1.8.



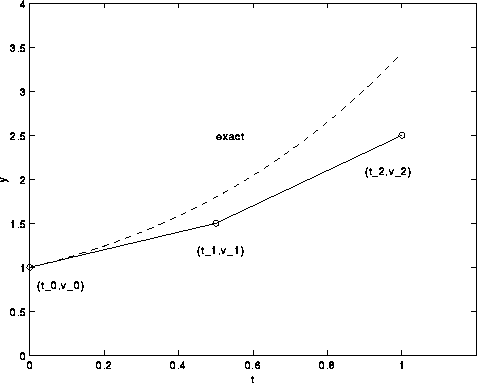
We compute v_2 using information at t_1.

Here h=t_2-t_1. The exact answer is y(1)=3.44.

We can write down a general formula for Euler's method. Suppose that the goal is to solve the ode

and to determine y(T).

• Discretize the interval [t_0,T]. Pick a bunch of points 0=t_0 < t_1 < t_2
  < ... t_N=T. They need not be equispaced.
• Let v_i denote the approximate solution at t_i. We have v_0=y_0, the
  given initial condition.
• Use the formula

  

  to compute approximate solutions for k=0,1,2, ...

A fundamental question at this point is: Does Euler's method work? Does the
approximate solution approach the exact solution as the number discretization
points increases? The answer is yes. The following table lists the approximate
answer at t=1 if N equispaced intervals are used. The exact solution is y(1)=3.44.

As we see, the error decreases as N increases. Note that error is approximately cut
in half when N is doubled. Euler's method has order of accuracy 1. A method has
order of accuracy p if

There many other numerical methods for computing approximate solutions to
differential equations. Some methods use information at several time steps to
compute a new approximation at t_k+1 (multistep methods). Other methods
compute v_k+1 from v_k in several stages (Runge-Kutta) methods.

Software for Solving Differential Equations Numerically

• Netlib: This is a repository for all sorts of mathematical software.
  Most of the programs are in C or Fortran. Look under ode or odepack.
• Consortium of Ordinear Differential Equations Experiments has reviews
  of various ode solvers for Macs, PCs, and other platforms.

[ODE Home] [1st-Order Home] [2nd-Order Home] [Laplace Transform Home] [Notation] [References]

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.