Last Ditch Effort

So, nothing has worked so far yet? Here are a few things to try. If you haven't done so yet, try checking to see if the limit of the terms is zero (the Divergence Test). Try splitting up a term into the sum of two different terms, and checking each separately, but be careful: if they both diverge, then the diverging parts may cancel each other out. If there is subtraction, and the parts being subtracted look similar, you might check for a Telescoping Series.

Still nothing? Does the series alternate betweeen positive and negative terms? You might try the Alternating Series Test. And, if you haven't tried it yet, try the Integral Test.

As an example, look at

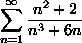
the sum over n from 1 to infinity of (n^2+2)/(n^3+6n)

The "highest power" method from the "no n powers" page will work, but let's use the Integral Test.

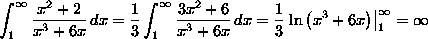
the integral from 1 to infinity of (x^2+2)/(x^3+6x) dx = 1/3 * the integral from 1 to infinity of (3x^2+6)/(x^3+6x) dx = 1/3 ln(x^3+6x) from 1 to infinity = infinity

So, since the corresponding integral doesn't converge, the series won't converge either.

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.