The Integral Test

If you can define f so that it is a continuous, positive, decreasing function from 1 to infinity (including 1) such that a[n]=f(n), then the sum will converge if and only if the integral of f from 1 to infinity converges.

For example, look at the sum

the sum over n from 1 to infinity of (n+1)/(n^2).

Does it converge? Well, define f(x) as follows

f(x) = (x+1)/(x^2)

and see if the integral converges.

the integral from 1 to infinity of (x+1)/(x^2) dx = the integral from 1 to infinity of (x+1)*x^(-2) dx = the integral from 1 to infinity of x^(-1) + x^(-2) dx =

ln(x) - x^(-1) from 1 to infinity = the limit as u goes to infinity of ln(u) - u^(-1) - ln(1) + 1^(-1) =

the limit as u goes to infinity of ln(u) - the limit as u goes to infinity of 1/u - 0 + 1 = the limit as u goes to infinity of ln(u) - 0 - 0 + 1 = infinity

The integral does not converge, so the sum does not converge either.

Remember, though, that the value of the integral is not the same as the sum of the series, at least in general. For instance,

the sum over n from 1 to infinity of (1/3)^(n-1) = 1/(1-1/3) = 1/(2/3) = 3/2

but

the integral from 1 to infinity of (1/3)^(x-1) dx = the integral from 1 to infinity of exp((x-1)*ln(1/3)) dx =

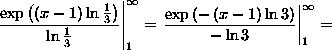
(exp((x-1)*ln(1/3)))/(ln(1/3)) from 1 to infinity = (exp(-(x-1)*ln(3)))/(-ln(3)) from 1 to infinity =

0-(exp(-0*ln(3)))/(-ln(3)) = 1/(ln(3)) which does not equal 3/2.

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.