Figure 7.1: The spacetime diagram for a traveling muon.

The lifetime of the muon must be measured in its own rest frame. Geometrically, we have the triangle in Figure 7.1, whose hypotenuse is $2c\times10^{-6}=600$ meters. The remaining leg of this 3–4–5 triangle is easily seen to be 1000 m, from which we can read off \begin{equation} \frac{v}{c} = \tanh\beta = \frac45 \end{equation}

1. According to earth clocks, when was the signal sent?
2. According to earth clocks, how long after the rocket left did the signal arrive back on earth?
3. According to the rocket observer, how long after the rocket left did the signal arrive back on earth?

Figure 7.2: The spacetime diagram for the rocket ship.

All of these questions can be answered by drawing a spacetime diagram, as shown in Figure 7.2. We again have a 3–4–5 triangle, with hypotenuse of length 1 and $\tanh\beta=\frac35$. We therefore have $\cosh\beta=\frac54$ (the vertical leg) and $\sinh\beta=\frac34$ (the horizontal leg). Thus, the signal was sent after $\frac54$ hours according to earth clocks, and received $\frac34$ hours after that, or 2 hours after the rocket left. To answer the final question, consider the large right triangle in Figure 7.2, also with (hyperbolic) angle $\beta$, and with vertical side 2. This side is the hypotenuse, since the right angle is in the upper right corner! We are trying to find the remaining side, which is $2\cosh\beta=\frac52$, so that the signal reaches earth $\frac52$ hours after the rocket left according to its own clocks.

 
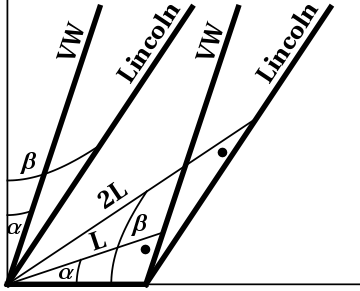
Figure 7.3: The spacetime diagram for the Lincoln and the VW.

Suppose the speed (really the rapidity) of the VW is given by $\tanh\alpha$ and that of the Lincoln is $\tanh\beta$. A spacetime diagram showing the worldlines of the front and back of each car is shown in the first diagram in Figure 7.3. Since the cars appear to be the same length, these worldlines intersect along the horizontal axis. The “true” lengths of the cars, namely $L$ and $2L$, respectively, are also shown. Comparing the right triangles shown, whose right angles are indicated with dots, and which share a common (horizontal leg), we see that \begin{equation} \frac{L}{\cosh\alpha} = \frac{2L}{\cosh\beta} \end{equation} so that \begin{equation} \cosh\beta = 2\cosh\alpha \end{equation} But we are given that $\tanh\alpha=\frac12$, so that, using the small triangles shown in the second diagram in Figure 7.3, we have in turn that \begin{eqnarray} \cosh\alpha &=& \frac{2}{\sqrt{3}} \\ \cosh\beta &=& \frac{4}{\sqrt{3}} \\ \tanh\beta &=& \frac{\sqrt{13}}{4} \end{eqnarray} so that the Lincoln is moving at $\frac{\sqrt{13}}{4}$ the speed of light.

 
Figure 7.4: The spacetime diagram for the scientist's analysis.

This situation is shown in Figure 7.4, from the shared reference frame of the clairvoyante (C) and her brother (B). The worldline of the scientist (S) is tilted to the right with (hyperbolic) angle $\beta$; his lines of simultaneity make the same angle with the horizontal axis. His time is measured along his own worldline, so we are looking for the “distance” between the two heavy dots. Triangle trigonometry does the rest; this leg has length \begin{equation} 500\sinh\beta = 1200 \hbox{km} \end{equation} where we have made use of the smaller 5–12–13 triangle shown in the figure to compute $\sinh\beta=\frac{12}{5}$ from $\tanh\beta=\frac{12}{13}$. Converting this to a time by dividing by $c$, we conclude that the scientist observes the brother hit his thumb $4\times10^{-3}$ seconds before Sophie cries out.