- §1. Practice
- §2. The Getaway
- §3. Angles are not Invariant
- §4. Interstellar Travel
- §5. Cosmic Rays
- §6. The Doppler Effect
Practice
-
In a laboratory experiment a muon is observed to travel 800 m before
disintegrating. The lifetime of a muon is $2\times10^{-6} \hbox{sec}$, so the speed must be \begin{equation} v = \frac{800 \hbox{m}}{2\times10^{-6} \hbox{sec}} = 4\times10^{8} \hbox{m/sec} \end{equation} which is faster than the speed of light! Identify the error in this
computation, and find the actual speed of the muon.
 Figure 7.1: The spacetime diagram for a traveling muon.
Figure 7.1: The spacetime diagram for a traveling muon.
The lifetime of the muon must be measured in its own rest frame. Geometrically, we have the triangle in Figure 7.1, whose hypotenuse is $2c\times10^{-6}=600$ meters. The remaining leg of this 3–4–5 triangle is easily seen to be 1000 m, from which we can read off \begin{equation} \frac{v}{c} = \tanh\beta = \frac45 \end{equation}
- A rocket ship leaves earth at a speed of $\frac35c$. When a clock on
the rocket says 1 hour has elapsed, the rocket sends a light signal back to
earth.
- According to earth clocks, when was the signal sent?
- According to earth clocks, how long after the rocket left did the signal arrive back on earth?
- According to the rocket observer, how long after the rocket left did the signal arrive back on earth?
 Figure 7.2: The spacetime diagram for the rocket ship.
Figure 7.2: The spacetime diagram for the rocket ship.
All of these questions can be answered by drawing a spacetime diagram, as shown in Figure 7.2. We again have a 3–4–5 triangle, with hypotenuse of length 1 and $\tanh\beta=\frac35$. We therefore have $\cosh\beta=\frac54$ (the vertical leg) and $\sinh\beta=\frac34$ (the horizontal leg). Thus, the signal was sent after $\frac54$ hours according to earth clocks, and received $\frac34$ hours after that, or 2 hours after the rocket left. To answer the final question, consider the large right triangle in Figure 7.2, also with (hyperbolic) angle $\beta$, and with vertical side 2. This side is the hypotenuse, since the right angle is in the upper right corner! We are trying to find the remaining side, which is $2\cosh\beta=\frac52$, so that the signal reaches earth $\frac52$ hours after the rocket left according to its own clocks.
- A Lincoln Continental is twice as long as a VW Beetle, when they are
at rest. As the Lincoln overtakes the VW, going through a speed trap, a
(stationary) policeman observes that they both have the same length. The VW
is going at half the speed of light. How fast is the Lincoln going?
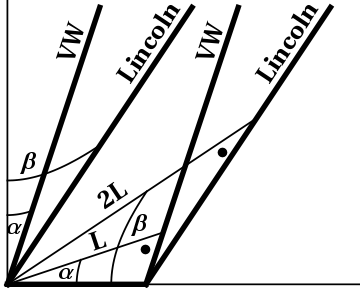

Figure 7.3: The spacetime diagram for the Lincoln and the VW.Suppose the speed (really the rapidity) of the VW is given by $\tanh\alpha$ and that of the Lincoln is $\tanh\beta$. A spacetime diagram showing the worldlines of the front and back of each car is shown in the first diagram in Figure 7.3. Since the cars appear to be the same length, these worldlines intersect along the horizontal axis. The “true” lengths of the cars, namely $L$ and $2L$, respectively, are also shown. Comparing the right triangles shown, whose right angles are indicated with dots, and which share a common (horizontal leg), we see that \begin{equation} \frac{L}{\cosh\alpha} = \frac{2L}{\cosh\beta} \end{equation} so that \begin{equation} \cosh\beta = 2\cosh\alpha \end{equation} But we are given that $\tanh\alpha=\frac12$, so that, using the small triangles shown in the second diagram in Figure 7.3, we have in turn that \begin{eqnarray} \cosh\alpha &=& \frac{2}{\sqrt{3}} \\ \cosh\beta &=& \frac{4}{\sqrt{3}} \\ \tanh\beta &=& \frac{\sqrt{13}}{4} \end{eqnarray} so that the Lincoln is moving at $\frac{\sqrt{13}}{4}$ the speed of light.
- Sophie Zabar, clairvoyante, cried out in pain at precisely the instant
her twin brother, 500 km away, hit his thumb with a hammer. A skeptical
scientist observed both events from an airplane traveling at $\frac{12{13}c$ to the right. Which event occurred first, according to the scientist? How much earlier was it?}


Figure 7.4: The spacetime diagram for the scientist's analysis.This situation is shown in Figure 7.4, from the shared reference frame of the clairvoyante (C) and her brother (B). The worldline of the scientist (S) is tilted to the right with (hyperbolic) angle $\beta$; his lines of simultaneity make the same angle with the horizontal axis. His time is measured along his own worldline, so we are looking for the “distance” between the two heavy dots. Triangle trigonometry does the rest; this leg has length \begin{equation} 500\sinh\beta = 1200 \hbox{km} \end{equation} where we have made use of the smaller 5–12–13 triangle shown in the figure to compute $\sinh\beta=\frac{12}{5}$ from $\tanh\beta=\frac{12}{13}$. Converting this to a time by dividing by $c$, we conclude that the scientist observes the brother hit his thumb $4\times10^{-3}$ seconds before Sophie cries out.