The unitary group $\SU(3)$ consists of all $3\times3$ unitary matrices with determinant $1$, that is \begin{equation} \SU(3) = \{M\in\CC^{3\times3}:M^\dagger M=1, |M|=1\} . \end{equation} The group $\SU(3)$ is the smallest of the unitary groups to be unrelated to the orthogonal groups; it's something new. As is the case for $\su(2)$, the Lie algebra $\su(3)$ consists of all $3\times3$ tracefree, anti-Hermitian matrices, that is \begin{equation} \su(3) = \{A\in\CC^{3\times3}:A^\dagger+A=0, \tr(A)=0\} . \end{equation}

The standard basis for the complexified Lie algebra $\su(3)\otimes\CC$ consists of the Gell-Mann matrices 1) \begin{align} \lambda_1 &= \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} ,\qquad \lambda_2 = \begin{pmatrix} 0 & -i & 0 \\ i & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} ,\nonumber\\ \lambda_3 &= \begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 0 \end{pmatrix} ,\qquad \lambda_4 = \begin{pmatrix} 0 & 0 & 1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \end{pmatrix} ,\nonumber\\ \lambda_5 &= \begin{pmatrix} 0 & 0 & i \\ 0 & 0 & 0 \\ -i & 0 & 0 \end{pmatrix} ,\qquad \lambda_6 = \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix} ,\nonumber\\ \lambda_7 &= \begin{pmatrix} 0 & 0 & 0 \\ 0 & 0 & -i \\ 0 & i & 0 \end{pmatrix} ,\qquad \lambda_8 = \frac1{\sqrt{3}}\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -2 \end{pmatrix} . \end{align} As with the Pauli matrices, the Gell-Mann matrices are Hermitian; unlike the Pauli matrices, they do not square to $\pm1$. However, they are again orthonormal with respect to the Killing form (with overall normalization $2$). We can obtain an anti-Hermitian basis of $\su(3)$ itself (that is, not complexified) by using the matrices \begin{equation} \mu_m = -i \lambda_m \end{equation} Alternatively, we can work with the real subset of these matrices, and study the real form $\sl(3,\RR)$ of $\su(3)$, that is \begin{equation} \sl(3,\RR) = \langle \lambda_1, \mu_2, \lambda_3, \lambda_4, \mu_5, \lambda_6, \mu_7, \lambda_8 \rangle \end{equation} where $\langle…\rangle$ denotes the span of the given elements, that is, the set of all linear combinations of these elements. By inspection, $\sl(3,\RR)$ contains 5 boosts and 3 rotations.

The given form of these matrices makes clear that $\lambda_3$ and $\lambda_8$ commute with each other, and that no larger set of basis elements will do so. The advantage of working with $\sl(3,\RR)$ is that these real symmetric matrices have real eigenvalues; at the Lie algebra level, their real eigenvectors will lie inside the algebra, without the need for complexification.

Explicitly, we have the commutation relations \begin{align} \lbrack\lambda_3,\lambda_8\rbrack &= 0 ,\nonumber\\ \left\lbrack\lambda_3,\frac12(\lambda_1\mp\mu_2)\right\rbrack &= \pm\frac22(\lambda_1\mp\mu_2) ,\quad \left\lbrack\lambda_8,\frac12(\lambda_1\mp\mu_2)\right\rbrack = 0 ,\nonumber\\ \left\lbrack\lambda_3,\frac12(\lambda_4\mp\mu_5)\right\rbrack &= \mp\frac12(\lambda_4\mp\mu_5) ,\quad \left\lbrack\lambda_8,\frac12(\lambda_4\mp\mu_5)\right\rbrack = \mp\frac{\sqrt{3}}2(\lambda_4\mp\mu_5) ,\nonumber\\ \left\lbrack\lambda_3,\frac12(\lambda_6\mp\mu_7)\right\rbrack &= \mp\frac12(\lambda_6\mp\mu_7) ,\quad \left\lbrack\lambda_8,\frac12(\lambda_6\mp\mu_7)\right\rbrack = \pm\frac{\sqrt{3}}{2}(\lambda_6\mp\mu_7) . \end{align}

Figure 2: The root diagram of $\su(3)$.

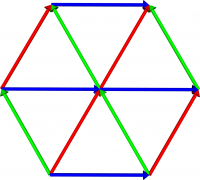
Regarding the eigenvalues as vectors in $\RR^2$, we can identify our basis elements with their eigenvalues, as follows: \begin{align} \frac12(\lambda_1\mp\mu_2) &\longleftrightarrow (\pm2,0) \nonumber ,\\ \frac12(\lambda_4\mp\mu_6) &\longleftrightarrow (\mp1,\mp3) \nonumber ,\\ \frac12(\lambda_6\mp\mu_7) &\longleftrightarrow (\mp1,\pm3) , \end{align} and both $\lambda_3$ and $\lambda_8$ correspond to $(0,0)$. As with $\su(2)$, we recover almost all of the structure of the Lie algebra by plotting these points. The result is shown in Figure 2, and is called the root diagram of $\su(3)$. Each family of parallel lines represents the action of one of the three pairs of eigenvectors on the other eigenvectors; again, the eigenvectors can be thought of as raising and lowering operators. It is a useful exercise to work out all the commutators, and to compare the result with the root diagram.