We begin this chapter with a motivating example. How do $\rhat$ and $\phat$ vary as you move from point to point? There are several ways to answer this question.

Figure 1: The polar basis vectors $\rhat$ and $\phat$ at three nearby points.

Figure 2: The change in $\rhat$ in the $\phi$ direction.

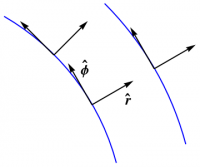
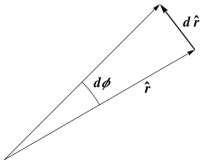
A geometric answer can be constructed by drawing $\rhat$ and $\phat$ at two nearby points, then comparing them. If the points are separated radially, it is clear that these basis vectors do not change as you move from point to point. Thus, along such a path, \begin{equation} d\rhat = 0 = d\phat \end{equation} What if you move through an angle $d\phi$ along a circle? It is now readily apparent that each basis vector is rotated through the same angle. Both of these possibilities are shown in Figure 1. Furthermore, the difference between two vectors of the same magnitude is a secant line on the circle connecting their tips, as shown in Figure 2 for $\rhat$; a similar construction holds for $\phat$. As the two vectors approach each other, this secant line becomes a tangent line, and is therefore perpendicular to the original vector. (An algebraic proof of this result is given below.) The magnitude of the difference between the two vectors is, in the limit, just the length of the arc between them, which, for unit vectors, is given by the angle. Thus, along such a path, \begin{align} d\rhat &= d\phi\,\phat \label{drh}\\ d\phat &= -d\phi\,\rhat \label{dph} \end{align} and these expressions in fact hold along any path, since radial motion does not contribute.

This answer can also be obtained by converting to rectangular basis vectors, which are constant; it is easy to differentiate vector fields in this basis! We have \begin{align} \rhat &= \cos\phi\,\xhat + \sin\phi\,\yhat \\ \phat &= -\sin\phi\,\xhat + \cos\phi\,\yhat \end{align} from which (\ref{drh}) and (\ref{dph}) easily follow by differentiation.

A somewhat more sophisticated argument begins by differentiating \begin{equation} \rr = r\,\rhat \end{equation} to obtain \begin{equation} d\rr = dr\,\rhat + r\,d\rhat \end{equation} and then comparing this result with the known (geometrically derived) formula \begin{equation} d\rr = dr\,\rhat + r\,d\phi\,\phat \end{equation} which verifies (\ref{drh}) immediately. We can determine $d\phat$ by noticing that \begin{equation} 0 = d(\phat\cdot\phat) = 2\,\phat\cdot d\phat \end{equation} so that, first of all, $d\phat$ has no $\phat$ component. More generally, this argument shows that any derivative of a vector of constant length must be perpendicular to the original vector. Furthermore, we have \begin{equation} 0 = d(\phat\cdot\rhat) = d\phat\cdot\rhat + \phat\cdot d\rhat \end{equation} which tells us that the $\rhat$ component of $d\phat$ must be $-d\phi$. Putting these two facts together yields (\ref{dph}), as expected.