You are here: start » book » guidecontent » cross
We strongly discourage teaching, or even reviewing, the dot and cross products at the same time — students tend to get them mixed up! The dot product is needed right away, in order to discuss line integrals, whereas the cross product isn't really needed until one discusses surface integrals. 1)
 Figure 9.3: The geometric definition of the cross product.
Figure 9.3: The geometric definition of the cross product.
The cross product is fundamentally a directed area. The magnitude of the cross product is defined to be the area of the parallelogram, as shown in Figure 9.3. This leads to the formula \begin{equation} |\vv\times\ww| = |\vv||\ww|\sin\theta \label{crossgeom} \end{equation} an immediate consequence of which is that \begin{equation} \vv\parallel\ww \Longleftrightarrow \vv\times\ww=\zero \label{Cross1} \end{equation} The direction of the cross product is given by the right-hand rule, so that in the example shown $\vv\times\ww$ points out of the page. This implies that \begin{equation} \vv\times\ww = - \ww\times\vv \label{Cross2} \end{equation} so that the cross product is not commutative. 2) An important property of the cross product is that \begin{equation} \vv\times\vv = \zero \end{equation} which follows from either ($\ref{Cross1}$) or ($\ref{Cross2}$).
In terms of the standard orthonormal basis, the geometric formula quickly yields \begin{eqnarray} \ii\times\jj &=& \kk \nonumber\\ \jj\times\kk &=& \ii \\ \kk\times\ii &=& \jj \nonumber \end{eqnarray} This cyclic nature of the cross product can be emphasized by abbreviating this multiplication table as shown in Figure 9.4. 3) Products in the direction of the arrow get a plus sign; products against the arrow get a minus sign.
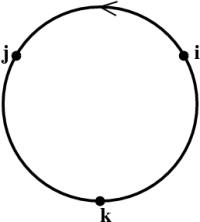 Figure 9.4: The cross product multiplication table.
Figure 9.4: The cross product multiplication table.
Using an orthonormal basis such as $\{\ii,\jj,\kk\}$, the geometric formula reduces to the standard component form of the cross product. If $\vv=v_x\,\ii+v_y\,\jj+v_z\,\kk$ and and $\ww=w_x\,\ii+w_y\,\jj+w_z\,\kk$, then 4) \begin{eqnarray} \label{CrossAlg} \vv\times\ww &=& (v_x\,\ii+v_y\,\jj+v_z\,\kk) \times (w_x\,\ii+w_y\,\jj+w_z\,\kk) \\ &=& (v_y w_z - v_z w_y)\,\ii + (v_z w_x - v_x w_z) \,\jj + (v_x w_y - v_y w_x)\,\kk \end{eqnarray} which is often written as the symbolic determinant \begin{equation} \vv\times\ww = \left| \matrix{\ii& \jj& \kk\cr v_x& v_y& v_z\cr w_x& w_y& w_z\cr} \right| \label{CrossDet} \end{equation}
We emphasize that this works in any (right-handed) orthonormal basis. In cylindrical coordinates, not only is \begin{equation} \rhat\times\phat = \zhat \end{equation} but cross products can be computed as \begin{equation} \vv\times\ww = \left| \matrix{\rhat& \phat& \zhat\cr v_r& v_\phi& v_z\cr w_r& w_\phi& w_z\cr} \right| \end{equation} where of course $\vv=v_r\,\rhat+v_\phi\,\phat+v_z\,\zhat$ and similarly for $\ww$.
We strongly discourage students from memorizing ($\ref{CrossAlg}$), recommending ($\ref{CrossDet}$) instead. But we discourage students from working out the determinant using minors, which would result in the final expression in ($\ref{CrossAlg}$) but with 2 sign changes in the term involving $\jj$. Instead, we encourage students to take $3\times3$ determinants in the form 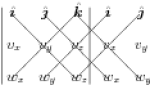 \begin{eqnarray} \end{eqnarray} where one multiplies the terms along each diagonal line, subtracting the products obtained along lines going down to the left from those along lines going down to the right. While this method works only for ($2\times2$ and) $3\times3$ determinants, and is therefore usually omitted from a linear algebra course, it has the definite advantage of emphasizing the cyclic nature of the cross product — whereas students who use minors often make sign errors.
\begin{eqnarray} \end{eqnarray} where one multiplies the terms along each diagonal line, subtracting the products obtained along lines going down to the left from those along lines going down to the right. While this method works only for ($2\times2$ and) $3\times3$ determinants, and is therefore usually omitted from a linear algebra course, it has the definite advantage of emphasizing the cyclic nature of the cross product — whereas students who use minors often make sign errors.
More important than which method students use to compute determinants is encouraging them not to use determinants at all for simple cross products, such as $(\ii+3\,\jj)\times\kk$, but instead to use the multiplication table directly. It is also worth pointing out that the multiplication table and the determinant method generalize naturally to other orthonormal bases; all that is needed is to replace the rectangular basis $\{\ii,\jj,\kk\}$ by the one being used.
A good problem which emphasizes the geometry of the cross product is to find the area of the triangle formed by connecting the tips of the vectors $\ii$, $\jj$, $\kk$ (whose base is at the origin).