The cross product is fundamentally a directed area. The magnitude of the cross product is defined to be the area of the parallelogram, as shown in the figure above. This leads to the formula $$ |\vv\times\ww| = |\vv||\ww|\sin\theta $$ an immediate consequence of which is that $$ \vv\parallel\ww \Longleftrightarrow \vv\times\ww=\zero $$ The direction of the cross product is given by the right-hand rule, so that in the example shown $\vv\times\ww$ points out of the page. This implies that $$ \vv\times\ww = - \ww\times\vv $$ so that the cross product is not commutative. 1) An important property of the cross product is that $$ \vv\times\vv = \zero $$ which follows from any of the preceding three equations.

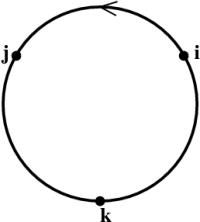
In terms of the standard orthonormal basis, the geometric formula quickly yields \begin{eqnarray*} \ii\times\jj &=& \kk \\ \jj\times\kk &=& \ii \\ \kk\times\ii &=& \jj \end{eqnarray*} This cyclic nature of the cross product can be emphasized by abbreviating this multiplication table as shown in the figure at the top of the page. 2) Products in the direction of the arrow get a plus sign; products against the arrow get a minus sign.

Using an orthonormal basis such as $\{\ii,\jj,\kk\}$, the geometric formula reduces to the standard component form of the cross product. If $\vv=v_x\,\ii+v_y\,\jj+v_z\,\kk$ and $\ww=w_x\,\ii+w_y\,\jj+w_z\,\kk$, then \begin{eqnarray} \vv\times\ww &=& (v_x\,\ii+v_y\,\jj+v_z\,\kk) \times (w_x\,\ii+w_y\,\jj+w_z\,\kk) \cr &=& (v_y w_z - v_z w_y)\,\ii + (v_z w_x - v_x w_z) \,\jj + (v_x w_y - v_y w_x)\,\kk \label{CrossAlg} \end{eqnarray} which is often written as the symbolic determinant \begin{equation} \vv\times\ww = \left| \matrix{\ii& \jj& \kk\cr \noalign{\smallskip} v_x& v_y& v_z\cr \noalign{\medskip} w_x& w_y& w_z\cr} \right| \label{CrossDet} \end{equation}

We emphasize that this works in any (right-handed) orthonormal basis. In cylindrical coordinates, not only is $$ \rhat\times\phat = \zhat $$ but cross products can be computed as $$ \vv\times\ww = \left| \matrix{\rhat& \phat& \zhat\cr \noalign{\smallskip} v_r& v_\phi& v_z\cr \noalign{\medskip} w_r& w_\phi& w_z\cr} \right| $$ where of course $\vv=v_r\,\rhat+v_\phi\,\phat+v_z\,\zhat$ and similarly for $\ww$.

We encourage you to use (\ref{CrossDet}), rather than simply memorizing (\ref{CrossAlg}). We also encourage you to compute the determinant as described below, rather than using minors; this tends to minimize sign errors. A $3\times3$ determinant can be computed in the form 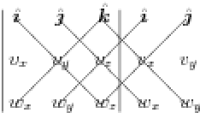where one multiplies the terms along each diagonal line, subtracting the products obtained along lines going down to the left from those along lines going down to the right. While this method works only for ($2\times2$ and) $3\times3$ determinants, it emphasizes the cyclic nature of the cross product.

Another important skill is knowing when not to use a determinant at all. For simple cross products, such as $(\ii+3\,\jj)\times\kk$, it is easier to use the multiplication table directly. It is also worth pointing out that the multiplication table and the determinant method generalize naturally to other orthonormal bases; all that is needed is to replace the rectangular basis $\{\ii,\jj,\kk\}$ by the one being used (in the right order!).

A good problem emphasizing the geometry of the cross product is to find the area of the triangle formed by connecting the tips of the vectors $\ii$, $\jj$, $\kk$ (whose base is at the origin).