You are here: start » book » physics » ringlimithint
Wrap-Up: The Ring: Limits Near and Far
The integral that you found in § {Activity: A Uniformly Charged Ring} is, in general, an elliptic integral. It cannot be evaluated in closed form other than to say that its value is the value of that integral. You can look up the value in a table (the old-fashioned way) or get a computer algebra package to compute the value for you (the modern way), but in either case, you do not get an answer which you can easily vary from point to point. See the Mathematica notebook
$\qquad\qquad\qquad\qquad$ Scalar Potential of a Continuous Ring
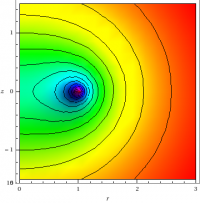
for a graphical approach using computer algebra, leading to Figure 1.
To get a better feel for the value of the integral, we consider some special cases. First of all, let's determine the potential along the axis. In this case, $\rr$ and $\rrp$ form the legs of a right triangle, with lengths $|\rr|=|z|$ and $|\rrp|=R$, respectively. This implies that \begin{eqnarray*} |\rr-\rrp| = \sqrt{R^2+z^2} \end{eqnarray*} which brings the integral to the form \begin{eqnarray*} V(z) = \Int_0^{2\pi} {1\over 4\pi\epsilon_0} {\lambda\,R\,d\phi'\over\sqrt{R^2 + z^2}} = {1\over 4\pi\epsilon_0} {2\pi\lambda\,R\over\sqrt{R^2 + z^2}} = {1\over 4\pi\epsilon_0} {Q\over\sqrt{R^2 + z^2}} \end{eqnarray*} where $Q = 2\pi R\lambda$ is the total charge on the ring.
It is instructive to consider the limiting case when $z=0$, which yields \begin{eqnarray} V(0) = {1\over 4\pi\epsilon_0} {Q\over R} \label{ringz0} \end{eqnarray} which is what one expects, since all of the charge is a distance $R$ from the origin.
What about the limit as $z\to0$? If $z\ll R$, we have \begin{eqnarray*} {1\over\sqrt{R^2 + z^2}} = {1\over R\sqrt{1+{z^2\over R^2}}} = {1\over R} \left( 1 - {1\over2} {z^2\over R^2} + {3\over8} {z^4\over R^4} - … \right) \end{eqnarray*} and we have \begin{eqnarray*} V(z) = {Q\over 4\pi\epsilon_0} \left({1\over R} - {1\over2} {z^2\over R^3} + {3\over8} {z^4\over R^5} - … \right) \end{eqnarray*} which of course agrees with our previous calculation ($\ref{ringz0}$) for $z=0$.
Consider the first two terms of this expansion for small $z$. There is no linear term, which means that the potential has a max or a min at $z=0$; this is an equilibrium point. Including the quadratic term results in a parabola — which opens up or down depending on the sign of $Q$. Choosing $Q>0$ corresponds to a situation with like charges, and like charges repel; a positively charged particle placed along the $z$-axis near the origin will be repelled away from the plane of the ring. The origin is therefore an unstable equilibrium point; the parabola opens downwards. Conversely, $Q<0$ corresponds to opposite charges, which attract; such a particle would be attracted towards the origin, and would oscillate back and forth through the origin. In this case, the origin is a stable equilibrium point; the parabola opens upwards.
Another interesting limit is $z\to\infty$; what happens then? If $z\gg R$, then \begin{eqnarray*} {1\over\sqrt{R^2 + z^2}} = {1\over z} {1\over\sqrt{1+{R^2\over z^2}}} = {1\over z} \left( 1 - {1\over2} {R^2\over z^2} + {3\over8} {R^4\over z^4} - … \right) \end{eqnarray*} so that \begin{eqnarray*} V(z) = {Q\over 4\pi\epsilon_0} \left({1\over z} - {1\over2} {R^2\over z^3} + {3\over8} {R^4\over z^5} - … \right) \end{eqnarray*} The leading term is now \begin{eqnarray*} V(z) \approx {1\over 4\pi\epsilon_0} {Q\over z} \end{eqnarray*} which is just the potential due to the total charge; to this order, the ring structure is not apparent. Furthermore, the next order term ($1\over z^2$) is zero; there is no dipole term, which makes sense, since the ring only has positive charge.