Gauss' Law
Gauss's Law says that a geometric property of the electric field (namely the flux through a particular closed surface) is the same as the charge enclosed by that same surface (divided by $\epsilon_0$ in the system of units that we are using): \begin{eqnarray*} \oint_{\hbox{closed surface}} \EE \cdot d\AA = \frac{1}{\epsilon_0} \, Q_{\hbox{enclosed}} \end{eqnarray*}
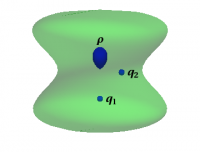
This situation is illustrated in Figure 1, which shows an arbitrary region containing two point charges, $q_1$ and $q_2$, as well as a third region with nonzero charge density, $\rho$. In this case, $Q_{\hbox{enclosed}}$ would be the result of adding the sum of the point charges to the total charge in the third region.
Gauss's law is a physically observed law which is true for any static charge distribution, discrete or continuous. The closed surface that is referred to in the law is not the boundary surface for a physical object, but rather any abstract (closed) surface that you can imagine. There is no problem with the law if there are also charges that are outside the surface. Such sources will contribute to the electric field, but when you sum up the flux across the whole surface, the contributions from charges outside the surface will cancel. Notice that a consequence of Gauss's Law is that the flux of the electric field through two surfaces is the same if they enclose exactly the same charge distribution.
As an example, consider a point charge $q$ inside an imaginary sphere of radius $r$, as shown in Figure 2. The electric field due to the charge is \begin{eqnarray*} \EE = \frac{1}{4\pi\epsilon_0} \frac{q}{r^2}\, \rhat \end{eqnarray*} and the surface element is \begin{eqnarray*} d\AA = r^2 \sin\theta \,d\theta\,d\phi\,\rhat \end{eqnarray*} Thus, the flux is given by \begin{eqnarray*} \Int_{\hbox{sphere}} \EE \cdot d\AA &=& \Int_{\hbox{sphere}} \frac{1}{4\pi\epsilon_0} \frac{q\,\rhat}{r^2} \cdot \rhat\,dA \\ &=& \frac{1}{4\pi\epsilon_0} \frac{q}{r^2} \times (\hbox{surface area}) \\ &=& \frac{q}{\epsilon_0} \end{eqnarray*} as claimed. (Why was it ok to replace the integral with the surface area?) Note that the value of this integral does not depend on the radius $r$ of the spherical surface.