The Relationship between Electrostatic Potentials, Fields, and Sources
Starting with the electrostatic potential for a point charge, we used the superposition principle in § {Potentials from Continuous Charge Distributions} to obtain an integral formula for the potential due to any continuous charge distribution, namely \begin{equation} V(\rr) = \int\limits_{\hbox{all charge}} {1\over 4\pi\epsilon_0} {\rho(\rrp)\, \delta\tau'\over|\rr-\rrp|} \end{equation} We also obtained a similar formula for the electric field in in § {Electric Fields from Continuous Charge Distributions}, namely \begin{equation} \EE(\rr) =\int\limits_{\hbox{all charge}} {1\over 4\pi\epsilon_0} {\rho(\rrp)\,(\rr-\rrp)\,\delta\tau'\over|\rr-\rrp|^3} \end{equation} These relationships correspond, respectively, to the arrows numbered 1 and 2 in Figure 1. 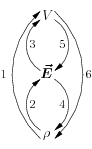 Figure 1: The relationships between $V$, $\EE$, and $\rho$. Each numbered
arrow is discussed in the text; moving down the diagram
corresponds to differentiation.
Figure 1: The relationships between $V$, $\EE$, and $\rho$. Each numbered
arrow is discussed in the text; moving down the diagram
corresponds to differentiation.
Furthermore, as discussed in § {Electric Field}, the electric field is just (minus) the gradient of the potential, that is \begin{equation} \EE(\rr)=-\grad V(\rr) \label{EgradV} \end{equation} which, as discussed in § {Finding the Potential from the Electric Field}, can be inverted to obtain the potential as an integral of the electric field, namely \begin{equation} V(\rr) = -\int\limits_{\rr_0}^{\rr}\EE(\rr')\cdot d\rr' \end{equation} where $\rr_0$ is the point where you have chosen the potential to be zero and the integral is along any (definite) path from $\rr_0$ to $\rr$. These last two relationships are arrows 5 and 3, respectively. We have also seen in § {Differential Form of Gauss's Law} that the charge density can be recovered as the divergence of the electric field, namely \begin{equation} \frac{\rho}{\epsilon_0}=\grad\cdot\EE \label{rhodivE} \end{equation} which is arrow number 4.
It remains to show how to recover the charge density from the potential (arrow number 6), at which point we are able to compute any one of the quantities $\EE$, $V$, and $\rho$ from any of the others.
But from ($\ref{EgradV}$) and ($\ref{rhodivE}$) it is easy to compute \begin{equation} \frac{\rho}{\epsilon_0} = -\grad\cdot\grad V \end{equation} which is the desired relation; this is Poisson's equation.
The special case of Poisson's equation with no source, namely \begin{equation} \nabla^2 V = 0 \end{equation} is called Laplace's equation. This equation arises in many contexts, not just in electrodynamics.