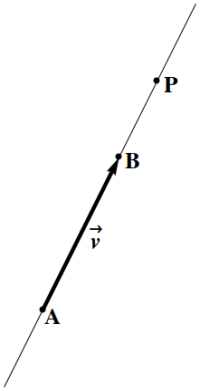
Two points $A$ and $B$ determine a line. But there are also other ways to describe a line. Rather than specifying two points, we can specify just one ($A$), then give a vector $\vv$ along the line.

Figure 1: The geometry behind the vector description of a line.

So let $\AA$ be the vector from the origin to the point $A$, and $\vv$ be a vector from $A$ that points along the line. Then any other point $P$ on the line can be reached by going to $A$ along $\AA$, then going along $\vv$. Thus, the vector \begin{equation} \rr(u) = \AA + \vv\,u \end{equation} from the origin to $P$ provides a vector parameterization of the line. Equivalently, if \begin{eqnarray} \AA &=& a_x\,\xhat + a_y\,\yhat + a_z\,\zhat \\ \vv &=& v_x\,\xhat + v_y\,\yhat + v_z\,\zhat \end{eqnarray} then the line is given by the parametric equations \begin{eqnarray} x &=& a_x + v_x\,u \\ y &=& a_y + v_y\,u \\ z &=& a_z + v_z\,u \end{eqnarray} which gives the coordinates $(x,y,z)$ of the point $P$ in terms of the parameter $u$. A given line can have many parametrizations, depending not only on the choice of the point $A$ on the line and vector $\vv$ along the line, but also on the choice of parameter $u$.

How do two points determine a line? Using vector addition, you can think of $\vv$ as $\BB-\AA$, and use the vector description above, as shown in Figure 1.

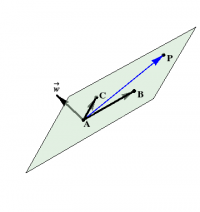
It takes three points $A$, $B$, $C$ to determine a plane, but again there are also other descriptions. The orientation of a line is given by a vector $\vv$ along the line. By contrast, the orientation of a plane is given by a vector $\ww$ perpendicular to the plane. A plane can therefore be specified by giving a point $A$ and a normal vector $\ww$ to the plane at the point $A$.

Figure 2: The geometry behind the vector description of a plane.

If $\rr$ is the vector from the origin to $P$, then $\rr-\AA$ is a vector in the plane, as shown in Figure 2. If $\ww$ is perpendicular to the plane, then it must be perpendicular to any vector in the plane. In particular, it must be perpendicular to $\rr-\AA$, so that \begin{equation} (\rr-\AA) \cdot \ww = 0 \end{equation} or equivalently \begin{equation} \rr \cdot \ww = \AA\cdot\ww \end{equation} Inserting the components \begin{eqnarray} \rr &=& x\,\xhat + y\,\yhat + z\,\zhat \\ \ww &=& w_x\,\xhat + w_y\,\yhat + w_z\,\zhat \end{eqnarray} and setting \begin{equation} d = \AA\cdot\ww = \hbox{constant} \end{equation} leads to \begin{equation} w_x x + w_y y + w_z z = d = w_x a_x + w_y a_y + w_z a_z \end{equation} for the equation of the plane through $A$ with normal direction $\ww$. This equation should look familiar! Note that the constant coefficients of this linear equation are precisely the components of the normal vector!

How do three points determine a plane? Using vector addition, you can construct two vectors in the plane, such as $\BB-\AA$ and $\CC-\AA$. The cross product of these vectors is perpendicular to the plane! Thus, set $\ww=(\BB-\AA)\times(\CC-\AA)$, and use the vector description above, as shown in Figure 2.