The same principles apply when integrating in higher dimensions: chop and add. For example, to find the amount of chocolate on a rectangular wafer given its (surface) mass density $\sigma$, first chop the plate into small rectangular pieces, as indicated symbolically in Figure 1. How big are the pieces? Surely \begin{equation} dA = dx \,dy = dy\,dx \end{equation}

Figure 1: Chopping a rectangular region.

What is the mass of each such piece? Clearly, $\sigma \,dA$. Since $\sigma$ is not constant, the total mass is given by \begin{equation} M = \int \sigma \,dA \end{equation} Since we are working in rectangular coordinates, we can write $\sigma=\sigma(x,y)$, so that the total mass is now 1) \begin{equation} M = \dint \sigma(x,y) \,dx\,dy \end{equation}

This is a double integral. How does one evaluate such an integral? Not surprisingly, one integrates twice.

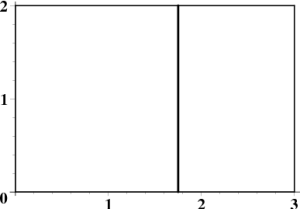
Consider the simplest case, when $\sigma$ is constant; if $\sigma=1$, this is equivalent to finding the area of the plate. Work from the inside out; this is an iterated single integral. Suppose one corner of the plate is at the origin, and the other at the point $(a,b)$ in the first quadrant. Then \begin{equation} M = \Int_{\hbox{plate}} \!\!\!dA = \Int_0^a \left( \Int_0^b \,dy\right) \,dx = \Int_0^a b \,dx = ab \end{equation} The integrals themselves are easy, but be careful to get the order of integration — and the limits — right. And the answer is, of course, no surprise.

Figure 2: Chopping a rectangular region first into vertical lines.

This integral corresponds to first slicing the rectangle into vertical lines of width $dx$, then breaking up each line into segments of length $dy$. One way to indicate this order is to draw a typical line in the region, as shown in Figure 2. The integration is performed in the reverse order: First add up the segments (integrate with respect to $y$), then the lines (integrate with respect to $x$). It is up to you to decide which way to chop first; the answer is the same either way.

In a case such as this one, where both the limits and the integrand are constant, the order simply doesn't matter. More generally, so long as the limits are constant, integrals of the form $\int f(x)\,g(y) \,dA$ can be factored, and the two pieces evaluated independently. For example, \begin{equation} \Int_2^3 \Int_1^2 xy \,dy\,dx = \Int_2^3 x\,dx \Int_1^2 y \,dy = \left(\frac{ x^2}{2}\right)\Bigg|_2^3 \left(\frac{ y^2}{2}\right)\Bigg|_1^2 = \frac{15}{4} \end{equation}