In § {Activity: Surface Elements on Planes, Cylinders and Spheres}, you should have obtained the following common surface elements: \begin{eqnarray*} \hbox{(plane) $\quad z={\rm const}$}: \qquad && d\SS=dx\,dy \>\zhat \\ \hbox{(plane) $\quad z={\rm const}$}: \qquad && d\SS=r\,dr\,d\phi \>\zhat \\ \hbox{(cylinder—top) $\quad z={\rm const}$}: \qquad && d\SS=r\,dr\,d\phi \>\zhat \\ \hbox{(cylinder—bottom) $\quad z={\rm const}$}: \qquad && d\SS=-r\,dr\,d\phi \>\zhat \\ \hbox{(cylinder—side) $\quad r={\rm const}$}: \qquad && d\SS=r\,d\phi\,dz \>\rhat\\ \hbox{(sphere) $\quad r={\rm const}$}: \qquad && d\SS=r^2\sin\theta\,d\theta\,d\phi \>\rhat \end{eqnarray*} where we must distinguish between the cylindrical coordinate $r$ (sometimes written as $s$) with its associated cylindrical basis vector \begin{equation} \rhat=\frac{x\,\xhat+y\,\yhat}{r} \end{equation} which points perpendicularly outward from the $z$-axis, and the spherical coordinate $r$ (sometimes written as $\rho$) with its associated spherical basis vector \begin{equation} \rhat=\frac{x\,\xhat+y\,\yhat+z\,\zhat}{r} \end{equation}

Figure 1: An upward-oriented disk.

Figure 2: A downward-oriented disk.

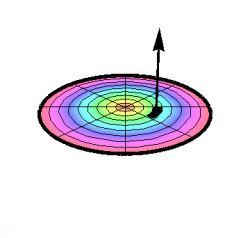
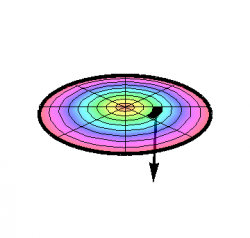
In each of these examples, the direction of the vector surface element is given by the basis vector associated with the coordinate that you held constant when describing the surface — up to sign. This sign corresponds to a choice about the orientation of the surface. The standard conventions, adopted above, are to orient the surface element outward for a closed surface such as a sphere, and upward otherwise, unless otherwise stated. In the absence of such a convention, each of the surface elements above would have to be preceded by a factor of $\pm1$. Compare Figures 1 and 2.

Figure 3: Chopping up a paraboloid in rectangular coordinates.

Figure 4: Chopping up a paraboloid in cylindrical coordinates.

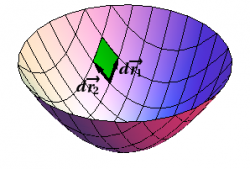
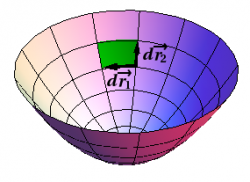
When using formula (1) of § {Activity: Surface Elements on Cylinders and Spheres}, the choice of orientation is determined by the order in which $d\rr_1$ and $d\rr_2$ are multiplied. By convention, one usually computes $d\AA=d\rr_1\times d\rr_2$, so the orientation is determined by the choice of which vector is $d\rr_1$, and which is $d\rr_2$. It is up to you to choose this labeling to correctly match the desired orientation. Which orientation is determined by the choices shown in Figures 3 and 4?

Formula (1) of § {Activity: Surface Elements on Cylinders and Spheres} will work for all kinds of complicated surfaces, so we wanted you to get practice in learning how to use it. However, when a surface can be described as a “coordinate equals constant” surface in an orthogonal coordinate system, then the cross product is trivial. You can think of the scalar area element as an infinitesimal “rectangle” whose area is just the product of the infinitesimal lengths of the two sides.