Curvilinear Coordinates
Choosing an appropriate coordinate system for a given problem is an important skill. The most frequently used coordinate system is rectangular coordinates, also known as Cartesian coordinates, after René Déscartes. One of the great advantages of rectangular coordinates is that they can be used in any number of dimensions.
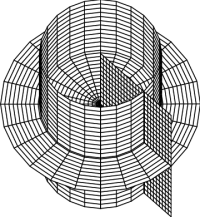
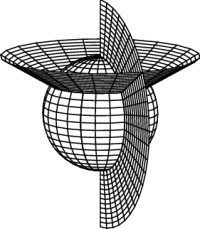
In three dimensions, holding any one coordinate fixed yields a surface, which is a plane in the case of rectangular coordinates. A coordinate system can be thought of as a collection of such “constant coordinate” surfaces, and the coordinates of a given point are just the values of those constants on the surfaces which intersect at the point. This is illustrated for rectangular coordinates in Figure 3.
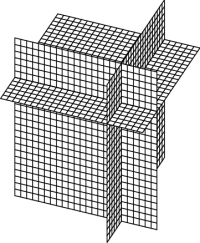 Figure 3: The coordinate planes in rectangular coordinates.
Figure 3: The coordinate planes in rectangular coordinates.
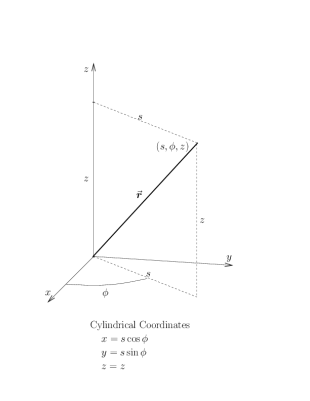
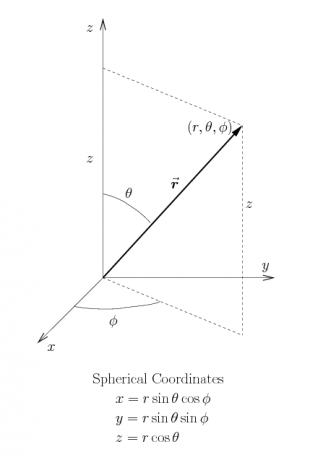
It is often useful, however, to use a coordinate system which shares the symmetry of a given problem — round problems should be done in round coordinates. The two standard “round” coordinate systems are cylindrical coordinates and spherical coordinates, as defined in Figure 4, and whose “constant coordinate” surfaces are shown in Figure 5. Either of these coordinate systems can also be restricted to the $xy$-plane, where they both reduce to polar coordinates. You should be aware that the standard physics conventions for cylindrical and spherical coordinates, used here, differ from the standard (American) math conventions; make sure you understand the difference.
The whole point of using curvilinear coordinates is that they are better adapted to the symmetries of the given problem. Ideally, this means that the entire problem should be done in curvilinear coordinates, without converting between coordinate systems, although this is not always possible. From this point of view, while it is certainly worth learning how to convert between, say, rectangular and polar coordinates, it is also worth learning how to avoid doing so as much as possible.
For completeness, the explicit transformations between these coordinate systems are given below. You should be able to use the diagrams in Figure 4 and trigonometry to verify these results. We reiterate that the conventions used here are “physicists' conventions”, used by almost everyone except American mathematicians. (For further discussion, see this article.)
Cylindrical Coordinates: \begin{eqnarray} x &=& r\cos\phi \qquad\qquad r^2 = x^2+y^2 \\ y &=& r\sin\phi \qquad\qquad \tan\phi = y/x \\ z &=& z \qquad\qquad\qquad\>\, z=z \end{eqnarray} Spherical Coordinates: \begin{eqnarray} x &=& r\sin\theta\cos\phi \qquad\qquad r^2 = x^2+y^2+z^2 \\ y &=& r\sin\theta\sin\phi \qquad\qquad \tan\theta = \sqrt{x^2+y^2}/z \\ z &=& r\cos\theta \qquad\qquad\qquad \tan\phi = y/x \\ \end{eqnarray}
Notice that $r$ in cylindrical coordinates indicates the horizontal coordinate distance from the $z$-axis, whereas $r$ in spherical coordinates indicates the radial coordinate distance from the origin. Other common conventions that you may see in other references include using $\rho$ (or $R$) for the spherical coordinate $r$ or using $s$ for the cylindrical coordinate $r$. 1)
We have labeled both of these coordinate systems so that they reduce to standard polar coordinates in the $xy$-plane, where $z=0$ and $\theta=\pi/2$. In both cases, $\phi$ is the angle around the $z$-axis. Make sure you know which geometric angles $\theta$ and $\phi$ represent, rather than simply memorizing their names. Whether or not you adopt the conventions used here, you should be aware that each of these labels is in common use for both of these angles, so that you will often see the roles of $\theta$ and $\phi$ interchanged.