The divergence and curl are traditionally defined by their component representations in rectangular coordinates. The Divergence Theorem and Stokes' Theorem are then statements about properties of the divergence and curl, respectively, which in turn lead to the geometric interpretation of divergence in terms of flux, and curl in terms of circulation.

This is backwards.

A better approach, promoted by Schey's classic book [ 5 ], is to define the divergence and curl in terms of the “theorems”, which are then merely definitions. The hard work, which used to go into proving the theorems, now goes into computing the formulas for the divergence and curl [ 5,6 ], Not only does this approach make the geometric interpretation obvious, it also makes clear, at least in principle, how to express the divergence and curl in other coordinate systems.

At any point $P$, we define the divergence of a vector field $\FF$, written $\grad\cdot\FF$, to be the flux of $\FF$ per unit volume leaving a small box around $P$. In order to compute the divergence, we must compute this flux. 1)

Consider a rectangular box whose sides are parallel to the coordinate planes. What is the flux of $\FF$ out of this box? Consider first the vertical contribution, namely the flux up through the top plus the flux down through the bottom. These two sides each have area element $dA=dx\,dy$, so we get \begin{eqnarray} \Int_{\rm top+bottom} \kern-15pt \FF\cdot d\AA &=& \DInt{R} \FF \bigg|_{\rm top}\kern-7pt\cdot\kk\> dx\,dy - \DInt{R} \FF \bigg|_{\rm bottom}\kern-22pt\cdot\kk\> dx\,dy \nonumber\\ &=& \DInt{R} \FF \bigg|_{\rm bottom}^{\rm top}\kern-22pt\cdot\kk\> dx\,dy \label{topbot1} \end{eqnarray} where $R$ denotes the common domain of the top and bottom faces in the $xy$-plane. Note the minus sign, which is really due to taking the dot product of $\FF$ with $-\kk$, which is the outward unit normal vector on the bottom face. But along any vertical line $C$ from the bottom face to the top face, we have \begin{equation} \FF \bigg|_{\rm bottom}^{\rm top}\kern-22pt\cdot\kk = F_z \bigg|_{\rm bottom}^{\rm top} = \Lint dF_z = \Lint \grad F_z \cdot d\rr = \Lint \Partial{F_z}{z} \,dz \label{Zmaster} \end{equation} where the second equality is the Fundamental Theorem of Calculus (“adding small changes yields the total change”), the next equality is the master formula (4) of Chapter 4, and the final equality follows since $d\rr=dz\,\kk$ for a vertical path.

Inserting ($\ref{Zmaster}$) into ($\ref{topbot1}$) results in \begin{equation} \Int_{\rm top+bottom} \kern-15pt \FF\cdot d\AA = \TInt{V} \Partial{F_z}{z} \>dz\,dx\,dy \end{equation} where $V$ denotes the volume inside the box. Repeating this argument using the remaining pairs of faces, it follows that the total flux out of the box is \begin{equation} {\rm total flux} = \Int_{\rm box} \FF \cdot d\AA = \Int_V \left( \Partial{F_x}{x} + \Partial{F_y}{y} + \Partial{F_z}{z} \right) \> dV \label{DivThm1} \end{equation}

We can use ($\ref{DivThm1}$) to compute the flux per unit volume through a small box around $P$. 2) Suppose the box is small enough that the expression in parentheses is nearly constant. We then get \begin{equation} {\rm total flux} \approx \left( \Partial{F_x}{x} + \Partial{F_y}{y} + \Partial{F_z}{z} \right) \Bigg|_P \> (\hbox{volume of $V$}) \end{equation} from which we see that the flux per unit volume, and hence the divergence, is given in rectangular coordinates by \begin{equation} \frac{\rm flux}{\rm unit volume} = \grad\cdot\FF = \Partial{F_x}{x} + \Partial{F_y}{y} + \Partial{F_z}{z} \end{equation}

Furthermore, we can construct an arbitrary box as a suitable combination of rectangular boxes, and the fluxes in ($\ref{DivThm1}$) on all interior sides will cancel, so that \begin{equation} \Int_{\rm box} \FF \cdot d\AA = \Int_{\rm inside} \kern-5pt \grad\cdot\FF \> dV \label{DivThm} \end{equation} We have proved the Divergence Theorem!

At any point $P$, we define the curl of a vector field $\FF$, written $\grad\times\FF$, to be the vector which gives the circulation of $\FF$ per unit area around an arbitrary small loop around $P$. That is, given any unit vector $\nn$ at $P$, $(\grad\times\FF)\cdot\nn$ should be the circulation of $\FF$ per unit area at $P$ around a small loop with axis $\nn$. 1) In order to compute the curl, we must compute the circulation around such loops.

Consider a rectangular loop in the $yz$-plane, with sides parallel to the coordinate axes. What is the circulation of $\FF$ around this loop?

Consider first the horizontal edges, on each of which $d\rr=dy\,\jj$, so that \begin{eqnarray} \Int_{\rm top+bottom} \kern-15pt \FF \cdot d\rr &=& - \Int_I \FF \bigg|_{\rm top}\kern-7pt\cdot\jj\> dy + \Int_I \FF \bigg|_{\rm bottom}\kern-22pt\cdot\jj\> dy \nonumber\\ &=& - \Int_I \FF \bigg|_{\rm bottom}^{\rm top}\kern-22pt\cdot\jj\> dy \label{topbot2} \end{eqnarray} where $I$ denotes the common domain of $y$ along the top and bottom edges. Note the counterclockwise orientation of the loop as seen from the positive $x$-axis; we are computing the $\ii$-component of the curl.

We can now insert ($\ref{Zmaster}$) into ($\ref{topbot2}$), except that we need the $\jj$-component of $\FF$ rather than the $\kk$-component, so that $F_z$ is replaced by $F_y$; this yields \begin{equation} \Int_{\rm top+bottom} \kern-15pt \FF \cdot d\rr = - \DInt{R} \Partial{F_y}{z} \>dz\,dy \end{equation} where $R$ denotes inside of the loop.

Repeating this argument for the remaining two sides, being careful with the orientation, leads to a similar term with $y$ and $z$ interchanged and with the opposite sign, so that the circulation around this loop is \begin{equation} \hbox{total $yz$-circulation} = \oint\limits_{\rm loop} \FF \cdot d\rr = \Int_R \left( \Partial{F_z}{y} - \Partial{F_y}{z} \right) dA \label{Vloop} \end{equation} where $dA=dy\,dz$.

Assuming that the loop is small enough so that the expression in parentheses is nearly constant yields an expression for the circulation per unit area around the loop, and hence the $\ii$-component of the the curl, namely 2) \begin{equation} \hbox{total $yz$-circulation} \approx \left( \Partial{F_z}{y} - \Partial{F_y}{z} \right) \> (\hbox{area inside loop}) \end{equation} so that \begin{equation} \frac{\hbox{$yz$-circulation}}{\rm unit  area} = (\grad\times\FF)\cdot\ii = \Partial{F_z}{y} - \Partial{F_y}{z} \end{equation} The rectangular expression for the full curl now follows by cyclic symmetry, yielding \begin{equation} \grad\times\FF = \left( \Partial{F_z}{y} - \Partial{F_y}{z} \right) \ii + \left( \Partial{F_x}{z} - \Partial{F_z}{x} \right) \jj + \left( \Partial{F_y}{x} - \Partial{F_x}{y} \right) \kk \end{equation} which is more easily remembered in the form \begin{equation} \grad\times\FF = \left| \matrix{\ii& \jj& \kk\cr \noalign{\smallskip} \Partial{}{x}& \Partial{}{y}& \Partial{}{z}\cr \noalign{\smallskip} F_x& F_y& F_z\cr} \right| \label{CurlDet} \end{equation}

It is not hard to show 3) that the circulation around any rectangular loop takes the form \begin{equation} \oint\limits_{\rm loop} \FF \cdot d\rr = \Int_{\rm inside} \kern-5pt (\grad\times\FF) \cdot d\AA \label{StokesThm} \end{equation} which of course reduces to ($\ref{Vloop}$) for the loop considered there. Furthermore, we can construct an arbitrary closed curve as a suitable combination of rectangular loops. Interior edges won't contribute to the total circulation, so that ($\ref{StokesThm}$) holds for any loop; this is Stokes' Theorem.

Applications in physics and engineering often involve high symmetry, and are therefore expressed in terms of an adapted orthonormal basis. We considered the gradient in §4.2 in Chapter 4; it is also useful to know the expressions for the divergence and curl in such bases. These formulas are usually looked up when needed; they can be found for instance on the inside front cover of some texts, such as Griffiths [ 6 ], and are reprinted at the end of this chapter. 1)

The most important thing to convey to students about these formulas is that they can not be derived using formal representations such as ($\ref{CurlDet}$). Why not? Because the basis vectors are no longer constant, so their derivatives matter. 2)

It is however fairly easy to work out these formulas if necessary. For instance, consider a radial vector field of the form \begin{equation} \HH = h( r )\,\rhat \end{equation} where $\rhat$ is the unit vector in the radial direction. The electric field of a point charge would have this form. What is the flux of $\HH$ through a small box around an arbitrary point $P$, whose sides are surfaces with one of the spherical coordinates held constant? Only the two sides which are parts of spheres contribute, and each such contribution takes the form \begin{equation} \Int_{\rm one face}\HH\cdot d\AA = \DInt{} h( r ) \,r^2\sin\theta\,d\theta\,d\phi \end{equation} Using an argument analogous to ($\ref{Zmaster}$) leads to \begin{equation} \Int_{\rm box}\HH\cdot d\AA = \TInt{} \Partial{}{r}\Bigl(r^2 h( r )\Bigr) \sin\theta\,dr\,d\theta\,d\phi = \int \frac{1}{r^2} \Partial{}{r}\Bigl(r^2 h( r )\Bigr) \,dV \end{equation} from which it finally follows that \begin{equation} \grad\cdot\HH = \frac{1}{r^2} \Partial{}{r}\Bigl(r^2 h( r )\Bigr) \end{equation}

Comparing with the formulas given at the end of the chapter, we see that this is just part of the full expression for the divergence in spherical coordinates, since we started with the very special vector field $\HH$. In practice, we would at most derive one such expression explicitly, which is enough to give the idea, then permit students to look up these formulas when needed.

The computations in this chapter, while geometric in origin, are still somewhat tedious. How then can one emphasize the geometry to students?

Technology can be used to explore the properties of different vector fields. One useful tool is the Vector Field Analyzer, a Java applet developed by Matthias Kawski [ 9 ], which makes a great classroom demo, and which can be made available for students to use outside of class. 1)

But first and foremost, show lots of pictures! Train students to look at plots of vector fields, and determine the divergence and curl qualitatively at various points — not just the origin, as is done in Group Activity 12 (Divergence & Curl). Make sure to emphasize that 2) \begin{eqnarray} {\rm divergence} &=& \frac{\rm flux}{\rm unit volume} \\ {\rm curl} &=& \frac{\rm circulation}{\rm (oriented)  unit  area} \end{eqnarray}

It helps students to have some experience using geometric arguments to think about the divergence and curl of different vector fields. In principle, one can use any shape box to calculate the flux, and any loop to calculate the circulation. In practice, it pays to pick a box that respects the symmetry of the given vector field, as discussed in the next two subsections.

Divergence

It can be useful to consider divergence in two dimensions, rather than three, since such vector fields are easier to visualize; the price is that such vector fields are usually less physical. In this context, divergence can be defined as the flux per unit area through a small (2-dimensional) box.

Figure 6.1: An axially symmetric vector field with vanishing flux.

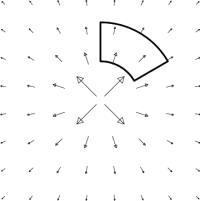
For example, for the vector field \begin{equation} \FF = \frac{x\,\ii+y\,\jj}{(x^2+y^2)} = \frac{\rhat}{r} \end{equation} which is axially symmetric, one should use a box adapted to polar coordinates, as shown in Figure 6.1. The box is pie-shaped, with the pointy end cut off in a circular arc (i.e. a big circular arc, a smaller circular arc closer to the origin, and two radial line segments that join the arcs). The magnitude of the vector field falls off like $\frac{1}{r}$ as you move radially outward from the origin, so one's first guess might be that the net flux is negative, that is, there is more flux into the box at the smaller radius than out of the box at the larger radius (and none through the sides). However, it turns out that the longer length of the latter side arclength exactly cancels this effect, since arclength is proportional to radius; the net flux is zero.

In three dimensions, the corresponding example is \begin{equation} \GG = \frac{x\,\ii+y\,\jj+y\,\kk}{(x^2+y^2+z^2)^{\frac32}} = \frac{\rhat}{\,r^2} \end{equation} which is spherically symmetric, and which falls off like $\frac{1}{r^2}$. The appropriate box for visualizing divergence is now a piece of a spherical shell, and the flux is only nonzero for the inner and outer faces of the box. The larger area of the outer face again exactly cancels the smaller magnitude of the vector field; the net flux is zero.

This only happens, of course, if the vector field falls off in exactly the right way; changing the power of $r$ in the denominator would lead to a nonzero flux. Remarkably, it is exactly the balanced case which occurs in the universe, both in electrostatics and in gravity. The electric field due to a point charge $q$ is \begin{equation} \EE = \frac{1}{4\pi\epsilon_0} \frac{q\,\rhat}{r^2} \end{equation} and the gravitational field due to a point mass $m$ is \begin{equation} \gv = G \, \frac{m\,\rhat}{r^2} \end{equation} where $\epsilon_0$ and $G$ are physical constants (which depend on the choice of units).

Furthermore, the laws of physics show that this same kind of detailed cancellation occurs whenever there is no charge density ($\rho_e=0$) or mass density ($\rho_m=0$). One of Maxwell's equations for electrostatics is \begin{equation} \grad\cdot\EE = \frac{1}{\epsilon_0} \rho_e \end{equation} and similarly for gravity \begin{equation} \grad\cdot\gv = 4\pi G \rho_m \end{equation} There may well be complicated electric fields in some region of space, but if there is no charge density at a given point, the divergence of the electric field will be zero there, so that the net flux of the electric field through any small box around that point will be zero. A similar statement can be made for the gravitational field.

This geometric fact leads to the convenient notion of field lines. If one draws throughout space a number of lines which is everywhere proportional to the amount of flux per unit area, then these lines can only begin and end at points where the divergence is nonzero, that is, where sources, such as charges or masses, exist.

Curl

Curl is circulation per unit area. More precisely, the circulation around a small loop, divided by the area of the loop, gives a good approximation to the component of the curl perpendicular to the loop. A good way to visualize circulation is to ask whether a paddle wheel (whose “handle” is perpendicular to the loop) will spin.

In practice, one often considers loops in coordinate planes such as the $xy$-plane, for which the circulation per unit area yields the $\kk$-component of the curl. For example, consider the vector field \begin{equation} \KK = \frac{-y\,\ii+x\,\jj}{(x^2+y^2)} = \frac{\phat}{r} \end{equation}

It seems clear that a paddle wheel at the origin will spin. If you put the paddle wheel in somewhere else, then there are long arrows pushing on the paddle closest to the origin and short arrows pushing on the paddle furthest from the origin, so one might expect the paddle wheel to spin. But there is a sense in which there are “more” arrows further from the origin. So more short arrows cancel fewer long arrows. It is hard with the paddle wheel picture to see how this goes quantitatively, so let's try to compute the circulation.

Figure 6.2: An axially symmetric vector field with vanishing curl.

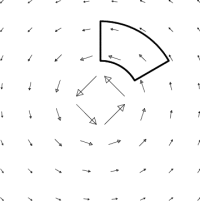
For this problem, it is easiest to use a pie-shaped loop, with the pointy end cut off as before, as shown in Figure 6.2. Now, $\KK$ is perpendicular to the radial line segments, which therefore don't contribute to the circulation. On each of the circular arcs, $\KK$ has constant magnitude and is parallel to the curve, so the line integral for these parts is just $|\KK|$ times the length of the arc. If the vector field falls off fast enough (magnitude gets smaller further from the origin), then the contribution from the big arc (smaller $|\KK|$, but larger arclength) is smaller than the contribution from the small arc (larger $|\KK|$, but smaller arclength) and the ($\kk$-component of the) curl will be negative. If the falloff is too slow, then the contribution from the larger arc will dominate and the ($\kk$-component of the) curl will be positive. For the particular falloff in this example, it turns out the contributions from the two arcs exactly cancel and the curl is precisely zero everywhere except at the origin.

Remarkably, the universe tends to pick out those cases which are balanced in this way. The magnetic field outside a current carrying wire is given by \begin{equation} \BB = {\mu_0 I\over2\pi} \frac{\phat}{r} \end{equation} where $\mu_0$ is a physical constant and $I$ denotes the current.

The laws of physics again show that this same kind of detailed cancellation occurs whenever there is no current. Another of Maxwell's equations is \begin{equation} \grad\times\BB = \mu_0 \JJ \end{equation} where $\JJ$ is the current density. There may well be complicated magnetic fields in some region of space, but if there is no current density at a given point, the curl of the magnetic field will be zero there, so that the net circulation of the magnetic field around any small loop around that point will be zero.

Below is a link to a page that summarizes the formulas for the gradient, divergence, and curl in rectangular, cylindrical, and spherical coordinates, as well as giving appropriate expressions for $d\rr$.

• Formula Sheet: Div, Grad, Curl