In §The Electric Field of a Uniform Disk, we found, by a round-about, complicated argument that the electric field due to an infinite, uniform plane of charge is give by \begin{eqnarray*} \EE(z) = \hbox{sgn}(z) \> \frac{\sigma}{2\epsilon_0}\,\zhat \end{eqnarray*} where the notation ${\rm sgn}(z)$ represents the sign of $z$. In cases like this, with very high symmetry, it is often simpler to use Gauss's law to find the electric field.

If you look at the formula for the integral form of Gauss's law in § {Gauss's Law}, namely \begin{eqnarray*} \oint_{\hbox{closed surface}} \EE \cdot d\AA = {1\over\epsilon_0} \, Q_{\hbox{enclosed}} \end{eqnarray*} you see that the electric field occurs in the integrand of an integral. In general, for an arbitrary surface and for an arbitrary field, the value and direction of the electric field will vary from point to point on the surface. So you can't, in general, use Gauss's law to find the value of the electric field. However, if you can find a suitable surface for which the component of the electric field normal (perpendicular) to the surface is either constant or zero everywhere on the surface, then you can pull this component of the electric field outside of the integral and solve for it.

An infinite plane of charge is highly symmetric. Not only is every point on the plane like every other, but also, at any given point on the plane, all directions in the plane are equivalent. This rotational symmetry means that, at all points above the plane, the electric field must be orthogonal to the plane. This fact probably seems obvious to you. But if we are trying find the electric field, then we actually need to prove this property.

How do we prove this statement? Using proof by contradiction. In a proof by contradiction, you assume the opposite of the thing you are trying to prove. Then you see what you can definitely say, based on this assumption, until you get to a statement that is clearly false. If you reach a false statement, then your original assumption must be false. Let's try it.

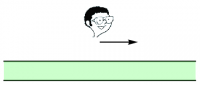
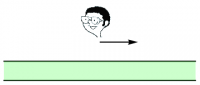
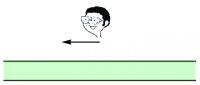
Figure 1: The symmetry argument used to show that the electric field points away from an infinite, uniformly charged plane. The observer in the first diagram, facing in the direction of a hypothetical tangential component of the field as shown by the arrow, expects to see the third diagram if he turns around, but instead sees the second.

Suppose that the electric field at a particular point above the plane had a component parallel to the plane. Let's call the direction of the electric field the $x$-direction. An observer, standing at this point, might initially face so as to see the electric field pointing straight in front of him, as shown in the first drawing in Figure 1. But, if that observer then turns in place to face a different direction, he would expect to see the electric field still pointing straight in front of him because of the symmetry of what he sees. Indeed, if he had been blindfolded when he turned, he could not tell, by looking at the charge distribution everywhere, that he had turned at all. This scenario is shown in the third drawing in Figure 1. Nevertheless, the fact that the observer has turned has not changed the electric field. If it initially had a component in the $x$-direction, it must still have a component in the $x$-direction. So the observer actually sees the situation depicted in the second drawing in Figure 1, which is not what he expected. The only way to resolve this contradiction is to recognize that our original assumption cannot be true. The electric field cannot have a component parallel to the plane. A similar argument using the translational symmetry, as shown in Figure 2, shows that the electric field can only depend on the distance from the plane. And another similar argument shows that the electric field must in fact point in opposite directions on opposite sides of the plane. The electric field must therefore be of the form \begin{eqnarray*} \EE = E(z) \, \zhat \end{eqnarray*} assuming that the $z$-direction is orthogonal to the plane.

Figure 2: Using symmetry to show translational invariance of the electric field.

Now recall Gauss' Law, which relates the flux of the electric field through any closed surface to the charge enclosed by the surface, that is, \begin{eqnarray*} \int \EE \cdot d\AA = \frac{q}{\epsilon_0} \end{eqnarray*} Choose a closed surface which exploits the symmetry. A rectangular box is one possibility, two of whose faces are parallel to the plane, and equidistant from it. The flux through the sides of this box is zero, since the normal vector to these sides is parallel to the plane, but $\EE$ is perpendicular to the plane, so that $\EE\cdot d\AA=0$. What about the top? The electric field is perpendicular to the top, but constant in magnitude. Thus, \begin{eqnarray*} \Int_{\hbox{top}} \EE \cdot d\AA = E(z) A \end{eqnarray*} where $z$ is the distance from the plane to the top of the box (where $z>0$). By symmetry, the flux through the bottom of the box is the same as that though the top. This implies that $E(-z)=-E(z)$. Finally, the charge enclosed by the box is just the charge density $\sigma$ times the area of the part of the plane inside the box, which is again $A$. Inserting all of this into Gauss' Law, we obtain \begin{eqnarray*} 2 E(z) A = \frac{\sigma A}{\epsilon_0} \end{eqnarray*} so that \begin{eqnarray*} E(z) = \frac{\sigma}{2\epsilon_0} \end{eqnarray*} which turns out to be independent of $z$ (for $z>0$).

What other charge densities are symmetric enough for you to use Gauss's law in this way? (There are only a few!)