Double Integrals in Polar Coordinates
Suppose you want to find the total mass of a round flat plate? How do you chop a round region?
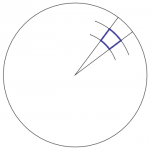
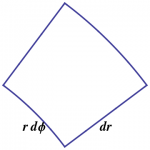
When working with round regions, it usually helps to use round coordinates! In polar coordinates, one chops a region into pie shaped regions using radial lines and circles, as shown in Figure 1. These lines are orthogonal to each other, so that a small enough piece is nearly rectangular, which means that its area is just its length times its width. As shown in Figure 2, a little thought shows that a radial side has length $dr$, but a circular side has length $r\,d\phi$ — not merely $d\phi$, which has the wrong units. Thus, in polar coordinates, 1) \begin{equation} dA = r \,dr \,d\phi \end{equation} Expressing the mass density in terms of polar coordinates, $\sigma=\sigma(r,\phi)$, then yields the total mass in the form \begin{equation} M = \int \sigma\,dA = \dint \sigma(r,\phi) \>r\,dr\,d\phi \end{equation}
For a round plate, the limits on this integral will be constant. The integral will be especially simple to evaluate if the density function is also round, that is, if $\sigma=\sigma(r)$ does not depend on $\phi$.
For example, suppose that the density is given by $\sigma=kr^2$, with $k$ constant. Then the mass of a circular plate of radius $R$ is \begin{eqnarray} M = \int_0^{2\pi} \int_0^R kr^2 r\,dr\,d\phi = (2\pi) k \left(\frac{R^4}{4}\right) = \frac{k\pi R^4}{2} \end{eqnarray}