Prerequisites
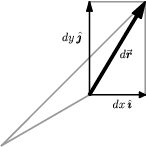
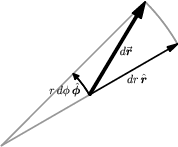
Expressing $d\rr$ in Other Coordinate Systems
Figure 1a:
The infinitesimal vector version of the Pythagorean Theorem
in rectangular coordinates.
It is important to realize that $d\rr$ and $ds$ are defined geometrically, not by the component expressions in equations (2) and (3) of § {The Vector Differential}. Because of this coordinate-independent nature of $d\rr$, it is possible and useful to study $d\rr$ in another coordinate system, such as polar coordinates ($r$,$\phi$) in the plane. 1) It is then natural to use basis vectors $\{\rhat,\phat\}$ adapted to these coordinates, with $\rhat$ being the unit vector in the radial direction, and $\phat$ being the unit vector in the direction of increasing $\phi$; see § {Activity: Curvilinear Basis Vectors}. 2)
Figure 1b:
The infinitesimal vector version of the Pythagorean Theorem,
in polar coordinates.
By determining the lengths of the sides of the infinitesimal polar “rectangle” shown in Figure 1b, one obtains \begin{equation} d\rr = dr\,\rhat + r\,d\phi\,\phat \label{dr2} \end{equation} Notice the factor of $r$ in the $\phat$ term; $d\phi$ by itself is not a length. The length of an infinitesimal arc is $r\,d\phi$. Using Equation (3) of § {The Vector Differential} to find the length of $d\rr$ as before leads to \begin{equation} ds^2 = dr^2 + r^2 \, d\phi^2 \label{ds2} \end{equation} which is the infinitesimal Pythagorean Theorem in polar coordinates.
1)
We choose $\phi$ for the polar angle in order to agree with the
standard conventions for spherical coordinates used by everyone but
(American) mathematicians.
2)
One can of course relate $\rhat$ and $\phat$ to $\xhat$ and $\yhat$,
for instance using the second figure in
Figure 2 of
§ {Wrap-Up: Curvilinear Basis Vectors}.
However, in most physical applications (as opposed to problems in calculus
textbooks) this step can be avoided by making an appropriate initial choice of
coordinates.