ANNOUNCEMENTS
MTH 437/537 — Spring 2017

6/19/17
I should be in my office today, from roughly 10 AM–2 PM, apart from a short lunch break.
6/15/17
The exams have been graded and course grades assigned.
You can collect your exam (and look at an answer key) anytime you can find me in my office...
6/11/17
Two minor comments on the exam:
6/10/17
Kidder is locked! If you can't get in:
(Kidder will likely also be locked tomorrow...)
6/7/17
As discussed in class on Monday, the Gödel geometry is described by the line element \begin{equation} ds^2 = -\left( dt + e^x dz \right)^2 + dx^2 + dy^2 + \frac12 e^{2x} dz^2 . \end{equation} This geometry satisfies $\vec{G} - \frac12 d\rr = \sigma^t \hat{e}_t$, corresponding to dust with energy density $\rho=1$, and with cosmological constant $\Lambda=-\frac12$. However, to justify the pictures shown in class requires a coordinate transformation: \begin{align} e^x &= \cosh(2r) + \cos\phi \,\sinh(2r) ,\\ z &= e^{-x} \sin\phi \,\sinh(2r) ,\\ t &= 2\sqrt2 \arctan\left(e^{-2r}\tan\frac\phi2\right) - \sqrt{2}\,\phi + 2\tau , \end{align} which brings the line element to the form \begin{equation} ds^2 = -\left(d\tau+\sqrt2\sinh^2(r)\,d\phi\right)^2 + dr^2 + dy^2 + \sinh^2(r)\cosh^2(r)\,d\phi^2 . \end{equation} The coefficient of $d\phi^2$ in this line element is \begin{equation} \sinh^2(r)\left(\cosh^2(r)-2\sinh^2(r)\right) = \sinh^2(r)\left(1-\sinh^2(r)\right), \end{equation} which changes sign where $\sinh(r)=1$, that is, where $r=\ln(1+\sqrt2)$. When $r$ has this value, the $\phi$ direction is null; when $r$ is larger than this value, the $\phi$ direction is timelike. But $\phi$ is periodic, so there are closed timelike (and null) curves purely in the $\phi$ direction.
6/5/17
The take-home final will be handed out in class on F 6/9, and will be due in my office at 11:30 AM on T 6/13.
The final covers Chapters 1–9 in the text.
It is fair to assume that all exam questions can be answered based on mastery of the material we have covered in class.
6/4/17
Here are my office hours for this week and next:
Students working on the take-home exam will have priority. Other times are possible by appointment.
6/2/17
The topics for next week's class are not yet set; the list on the schedule page should be treated as tentative. Feel free to send me comments regarding these or other topics, and if relevant the order in which you would like to see them covered.
5/29/17
I will be in my office tomorrow (Tuesday) from 1–2 PM.
Other times later in the day (most likely after 3 PM) may also be possible by appointment.
5/26/17
There is a nice discussion of Olber's paradox in §22.2 of d'Inverno's text, as well as on John Baez's website.
Olber's proposed resolution was to postulate the existence of an interstellar gas that would absorb radiation; this argument fails. The paradox holds regardless of whether the universe is Euclidean, or whether it is infinite. One possible resolution with a static universe is to assume that stars did not start radiating until recently, but some observed stars are too old. The accepted resolution is that an expanding universe causes a redshift in the observed frequency, which reduces the energy that reaches us.
5/24/17
There are several computer algebra packages available for computing curvature components:
Printouts of (old!) sample computer algebra sessions are available for GRTensor and CLASSI.
Older versions of my instructions, that also include coordinate-based computations, are available for Maple and Mathematica packages, and for SHEEP/CLASSI.
5/22/17
I will be late for my office hour on Wednesday, 5/24/17, due to a campus event ending at 2 PM.
I will likely be in my office Wednesday morning. Email me for an appointment, or drop by and take your chances.
5/15/17
There were several questions both during and after class regarding the derivation of the equation of geodesic derivation in the general case. As indicated in §7.3 of the text, a more detailed derivation is given in §A.2.
Derivatives of vector fields do not in general commute! As shown in class (but not clearly stated in §A.2), $\dot{\uu} = (\rr')\Dot = (\dot\rr)' = \vv'$ holds because the connection is assumed to be torsion free. But $\ddot\uu = (\vv')\Dot \ne (\dot\vv)'$, which would of course vanish by the geodesic equation.
5/12/17
As announced in class, there are minor typos in the Schwarzschild curvature 2-forms as given in §A.3 of the text.
The coordinate expressions in the middle of Equations (A.52) and (A.53) are each missing a factor of 1/2.
Also, the initial minus sign should be removed from Equation (A.61).
(The final expressions in terms of an orthonormal frame are correct.)
The wiki version has been corrected, and a full list of errata can be found here.
5/10/17
Further information about charged and rotating black holes and their Penrose diagrams can be found in the undergraduate textbook by d'Inverno, which is on reserve.
A more advanced treatment can be found in the book The Large Scale Structure of Space-Time by Hawking & Ellis, available in the library.
5/4/17
A formula sheet will be available on the midterm. You can find a copy here.
I should be in my office this afternoon from roughly 1:30–3:30 PM
5/1/17
In addition to my usual office hours this week (M 10:30–11:30 AM and WF 1:30–2:30 PM), I will also be in my office Wednesday morning from 9:30–11:30 AM, and Friday morning from 9:30–10:30 AM.
Other times may be possible; ask.
Reminder: there will not be any office hours next Monday.
4/30/17
The midterm will be Monday 5/8/17 in class. The main topics to be covered on the midterm are:
Further information:
I will hold extra office hours next week, most likely WF morning; other times will be available by appointment.
There will be no office hours on the day of the exam, nor can I guarantee a response to email messages received after Friday's class, although there's a good chance I will be able to respond Sunday evening. (My apologies; I will be out of town that weekend, and busy with OSU committee work as soon as I return.)
4/29/17
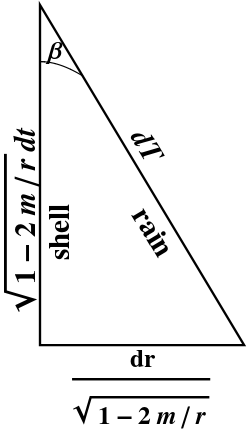
Figure 3.9 on page 38, showing the relationship between shell coordinates and rain coordinates, is correct but misleading.
This figure shows the relationships between certain differential forms, using the geometric description of §13.8, but without displaying the stacks. However, it is not easy in such diagrams to read off the magnitudes of the differential forms, which do not correspond directly to the lengths of the sides.
A more traditional figure, using the language of infinitesimal displacement, is shown at the right.
4/28/17
This week, we introduced the orthonormal 1-forms $\sigma^T$ and $\sigma^R$. Although we didn't work out all of the details in class, this basis leads to the orthogonal coordinates ($T$,$R$), known as rain coordinates, defined by \[ dT = dt + \frac{\sqrt{\frac{2m}{r}}}{1-\frac{2m}{r}} \>dr ; \qquad dR = dt + \frac{\sqrt{\frac{r}{2m}}}{1-\frac{2m}{r}} \>dr . \] [Note: The name "Painlevé-Gullstrand coordinates" usually refers to ($T$,$r$), rather than ($T$,$R$).]
In rain coordinates, the line element (with $\theta$ and $\phi$ held constant) takes the form \[ ds^2 = -(\sigma^T)^2 + (\sigma^R)^2 = -dT^2 + \frac{2m}{r} \,dR^2 \] from which it is again clear that the line element is well-behaved at $r=2m$. It is now also obvious that, as claimed in class, $T~$corresponds to the proper time of the freely-falling observer, since for such observers $R$ is constant. Finally, holding $T$ constant forces $dT=0$, so that $dt$ can be expressed in terms of $dr$, leading to $dR=\sqrt{\frac{r}{2m}}\,dr$, so that the (full) line element reduces to that of flat, Euclidean $\RR^3$. That is, the surfaces of simultaneity for a freely-falling observer are flat, as shown by a slightly different argument in class.
It is also possible to use this form of the line element to argue that the surfaces $\{r=2m\}$ are null, since $dT=dR$ in this limit. However, due to the poor behavior of the coordinate $t$ near $r=2m$, this particular argument is easier to make from the Painlevé-Gullstrand form of the line element, using $T$ and $r$ as coordinates.
4/26/17
In addition to the rain frame, adapted to freely-falling observers starting from rest at $r=\infty$, Taylor and Wheeler introduced the notion of a drip frame, adapted to freely-falling observers starting from rest at $r=r_0$ (and hence moving more slowly than "rain"), as well as a hail frame, adapted to freely-falling observers starting with an initial downward velocity at $r=\infty$ (and hence moving faster than "rain"). For further details, see EBH.
4/21/17
I almost got the algebra right in class today—I divided by $r$ instead of $m$ in one of the steps near the very end...
The correct answer was however given in class, and is Eq. (3.47) in the text.
4/20/17
With apologies, tomorrow afternoon's office hour is canceled.
I will be in my office most of the morning.
I should be in my office from roughly 9:30–10:45 AM and again from roughly 12:45–1:15 PM.
4/10/17
There was some confusion in class today regarding the notion of uniform acceleration. Both ends of an accelerating rocket experience the same acceleration. The gravitational analog is to regard the rocket sitting on its launchpad in Earth's (essentially) constant gravitational field, $g$. However, the gravitational potential is given by $gh$; it depends on the height. The conclusion is that clocks run slower when the gravitational potential is lower. This conclusion remains valid even when the field is not uniform; close to a massive object, clocks run slow.
4/10/17
One important theme in today's derivation of the geodesic equation is that differentials are the numerators of derivatives. Thus, an equation involving 1-forms can be converted to one involving derivatives by dividing by a differential.
A more subtle message is that this doesn't work for second derivatives. In particular, the geodesic equation is a second order system of ODEs, but there is no way to take two derivatives with respect to the same parameter using differential forms...
Also, the distances I initially gave as the answers to the second homework problem were indeed based on a typo at my end; sorry about that. The numbers we used instead were correct.
4/7/17
The slides from today's lecture are available here.
Further discussion of the twin paradox, including the cylindrical universe mentioned in class, can be found in §8.3 of my book on special relativity.
4/5/17
My office hours have now been posted on the course homepage.
In addition to the posted times, I am usually in my office MWF mornings from roughly 9:30–11:30 AM, and am also usually available both before and after class. Feel free to drop in at those times — or to contact me to arrange an appointment at these or other times.
3/31/17
I propose offering an optional "review" sessions, at a time to be arranged, in order to go over the final from MTH 434/534,
Please be prepared to discuss times for this session on the first day of class.
3/30/17
The primary text for this course will be my own book, which can be read online as an ebook through the OSU library.
There is also a freely accessible wiki version available, which is however not quite the same as the published version.
We will also refer briefly to my book on special relativity.
You may purchase this book if you wish, but it can also be read online as an ebook through the OSU library, and again there is also a wiki version.
You may also wish to purchase a more traditional text, in which case I recommend any of the first three optional texts listed on the books page. The level of this course will be somewhere between that of these books, henceforth referred to as EBH (Taylor & Wheeler), Relativity (d'Inverno), and Gravity (Hartle).
We will cover more material than EBH, but we will stop short of the full tensor treatment in Relativity or (the back of) Gravity. We will also cover some of the material on black holes from EBH which is not in Gravity or Relativity.
In short, none of these books is perfect, but all are valuable resources. In addition to the above books, OSU owns an electronic copy of Relativity Demystified, which summarizes many of the key aspects of relativity, but provides no derivations. By all means use it for reference, but I would not recommend using it as a primary text.