Models
for Water
A large number of 'hypothetical' models for
water have been developed in order to discover the structure
of water (for reviews of their development see [275],
for a review of their use in supercritical water see [433]
and for an appraisal of their accomplishments see [400]),
on the basis that if the (known) model (i.e. computer
water) can successfully predict the physical properties of
liquid water then the (unknown) structure of liquid water
is determined. They involve orienting electrostatic effects
and Lennard-Jones sites that may or may not coincide with
one or more of the charged sites. The Lennard-Jones interaction
accounts for the size of the molecules. It is repulsive at
short distances, ensuring that the structure does not completely
collapse due to the electrostatic interactions. At intermediate
distances it is significantly attractive but non-directionala and competes with the directional attractive electrostatic
interactions. This competition ensures a tension between an
expanded tetrahedral network and a collapsed non directional
one (e.g. similar to that found in liquid
noble gases). Generally each model is developed to fit
well with one particular physical structure or parameter (e.g. the density anomaly, radial
distribution function or the critical
parameters) and it comes as no surprise when a model developed
to fit certain parameters gives good compliance with these
same parameters (e.g. see [984]).
It is also the case that, in spite of the heavy computational
investment in the calculations, the final agreement (or otherwise) with
experimental data is often 'by eye' and not statistically tested or
checked for parametric sensitivity. Also, tests for 'fit' often seem to
be completed with publication in mind rather than rigor; thus many
papers use the radial distribution fit with diffraction data as their
'gold standard' in spite of the major fitted peaks (where the agreement
looks so impressive 'by eye') being derived from the tetrahedral nature
of water that is built into every model and overpowering any
disagreement in the fine detail. Also unfortunately, the purity, isotopic mix and perhaps even the ortho/para spin state present in real water may cause
difficulty over choice of the value of the physical parameter
[400],
as models only utilize one isotopic form and ignore the spin state and
the presence of other entities such as ions. Also, there is still
disagreement over which value of some physical parameters to use, e.g. for the dipole moment. Whether model
results agree with other physical properties of water then
acts as proof (or otherwise) of their utility. By and large,
the more fitting parameters that are required by the model
(and some require over 50), the better the fit. Some models
show a lack of robustness due to their sensitivity to the
precise model parameters [206],
the system size or the calculation method [619, 649]. A study
of sensitivity of water's behavior with respect to changes
in the parameters using the TIP4P model potential showed that σ,
followed by the O-H bond length, had the major effects on
the density, enthalpy of vaporization and radial distribution
function fits [494].
A separate sensitivity analysis showed that the thermodynamic
properties of water models were most sensitive to the van der Waals
repulsive, the short range Coulomb and the polarization components of
the potential [1042].
It can be noted that a number of these models use water molecules
with a wider (tetrahedral) H-O-H angle and longer H-O bond
length than those expected of gaseous or liquid water and indicative of the importance
of including parameters giving strong hydrogen bonding. Water
molecules in liquid water are all non-equivalent (differing
in their molecular orbitals, their precise geometry and molecular
vibrations; for an extreme case see the water
dimer) due to their hydrogen bonding status, which is
influenced by the arrangement of the surrounding water molecules.
Some models are polarizable [867]
to make some allowance for this,c,d whereas other simpler models try to reproduce 'average' structures.
| A recent review listed 46
distinct models [400], so
indirectly indicating their lack of success in quantitatively
reproducing the properties of real water. They may,
however, offer useful insight into water's behavior.
Some of the more successful simple models are opposite
with their parameters given below.
Models types a, b and c are all planar whereas type d is almost tetrahedral |
|
Model |
Type |
σ Å 6 |
ε kJ mol-1 6 |
l1 Å |
l2 Å |
q1 (e) |
q2 (e) |
θ° |
φ° |
|
-8 |
3.016 |
15.319 |
- |
- |
- |
- |
109.47 |
109.47 |
|
a |
3.166 |
0.650 |
1.0000 |
- |
+0.410 |
-0.8200 |
109.47 |
- |
|
a |
3.166 |
0.650 |
1.0000 |
- |
+0.4238 |
-0.8476 |
109.47 |
- |
|
a |
3.166 |
0.650 |
1.0000 |
- |
+0.4350 |
-0.8700 |
109.47 |
- |
|
a |
3.166 |
0.650 |
1.0120 |
- |
+0.410 |
-0.8200 |
113.24 |
- |
|
a |
3.15061 |
0.6364 |
0.9572 |
- |
+0.4170 |
-0.8340 |
104.52 |
- |
|
a |
3.1506 |
0.6368 |
0.9600 |
- |
+0.4170 |
-0.8340 |
104.5 |
- |
|
b |
3.23400 |
0.6000 |
0.9430 |
0.06 |
+0.5170 |
-1.0340 |
106.00 |
127.00 |
|
c |
3.15365 |
0.6480 |
0.9572 |
0.15 |
+0.5200 |
-1.0400 |
104.52 |
52.26 |
|
c |
3.16435 |
0.680946 |
0.9572 |
0.125 |
+0.52422 |
-1.04844 |
104.52 |
52.26 |
|
c |
3.15365 |
0.6480 |
0.9572 |
0.15 |
+0.631 |
-1.261 |
104.52 |
52.26 |
|
c |
3.1668 |
0.8822 |
0.9572 |
0.1577 |
+0.5897 |
-1.1794 |
104.52 |
52.26 |
|
c |
3.1589 |
0.7749 |
0.9572 |
0.1546 |
+0.5564 |
-1.1128 |
104.52 |
52.26 |
|
c |
four terms used |
0.9681 |
0.141,3 |
+0.6213 |
-1.2459 |
102.71 |
51.351 |
|
c |
3.17459 |
0.9445 |
1.0000 |
0.15 |
+0.450672 |
-0.901344 |
109.47 |
- |
|
c |
3.69 4,11 |
0.9146 4 |
0.9572 |
0.27 |
+0.6113 |
-1.2226 |
104.52 |
52.26 |
|
c |
3.18395 |
0.88257 |
0.9572 |
0.24034 |
0.55733 |
-1.11466 |
104.52 |
52.26 |
|
d |
3.10000 |
0.31694 |
1.0000 |
0.80 |
+0.24357 |
-0.24357 |
109.47 |
109.47 |
|
d |
3.12000 |
0.6694 |
0.9572 |
0.70 |
+0.2410 |
-0.2410 |
104.52 |
109.47 |
|
d |
3.097 |
0.7448 |
0.9572 |
0.70 |
+0.2410 |
-0.2410 |
104.52 |
109.47 |
|
c |
five parameters used |
0.9572 |
0.70 |
+0.574 |
-1.148 |
104.52 |
52.26 |
|
d |
2.9837 4 |
4 |
0.9572 |
0.5 |
varies 5 |
-0.42188 |
104.52 |
109.47 |
|
c/d7 |
3.115OO
0.673HH |
0.715OO
0.115HH |
0.980 |
0.8892L
0.230M |
+0.477 |
-0.044L
-0.866M |
108.00 |
111.00 |
1 Average values; 2 Polarizable models; 3 charge = -2.48856; 4 Buckingham potentiala, This exponential potential presents a more flexible (i.e. softer)
surface compared with the Lennard-Jones r-12 interaction.; 5 with charge on oxygen
atom; 6σ and ε are Lennard-Jones parameters. The separation and depth of
the potential energy minimum between two similar molecules
(equivalent to diameter); 7 has charges on the lone pair sites (L) as in model
type d and the mid-point site (M)
as in model type c; 8 has only a single, center of mass, interaction site with a
tetrahedrally coordinated sticky potential that regulates
the tetrahedral coordination of neighboring molecules; 9 a polarization charge qpol (-8) is connected by
a spring to site q2, the total charge (qpol+q2)
being given in the table as q2; 10 The charges are smeared (i.e. not point charges)
using Gaussian distributions with widths of 0.455 Å
and 0.610 Å for q1 and q2 respectively; 11 Zero potential position at 3.25 Å. 12 This model over-structures the water. 13 A 'Drude' particle carrying a negative charge -1.71636e is
attached by a harmonic spring (4184 kJ mol-1 Å-2 while the oxygen carries a charge +1.71636e. 14
Induced dipoles are placed on the atoms. The van der Waals terms give a
deeper, steeper and more distant energy minimum (-1.187 kJ mol-1 at 3.726 Å) than the typical Lennard-Jones potential. [Back] 
Some of the above values are varied slightly
by different workers. Other workers use diffuse electron density
[203] or polarizable
versions of the non-polarizable models, using flexible bonding
(e.g. SWFLEX-AI),
induced dipoles (e.g. [181]),
energy optimization (e.g. the TIP4P-FQ version of TIP4P) or movable charge (e.g. SWFLEX-AI),
all of which generally give better fit but at a significantly
increased computational cost [198].
Polarization mutually strengthens the hydrogen bonding and
partially compensates for the absence (except statistically)
of the known long range interactions and the dependence of
these models on short-ranged forces. Diffuse electron density
[203] varies the effective charges
with distance. Such models generally perform better away from
the ambient conditions under which they are parameterized
than the simpler models.
Some of the calculated
physical properties of the water models.
All the data is at 25°C and 1 atm, except * at 20°C
and ** at 27°C.
Many of the data values given in the table vary significantly between different workers (see e.g. [185]). A comparison of some of
the properties of the gas phase dimers for various models
are given in a recent paper [704].b As can be deduced from the data given (and other data), although
such simple models are of great utility, no universally applicable
model can be identified at this time. It should also be noted
that many simulations are performed with just a few hundred
water molecules within rectangular periodic boxes no more
than 2.5 nm along each edge for times equivalent to a few
picoseconds; conditions that reduce discovery of long-range
effects and introduce artifacts. Use of cut-off lengths (even
long ones) in the intermolecular interactions may also introduce
artifacts [761].
It should be noted that there is a strong correlation between
the length scale of any water structuring and the time scale
which is required to see it. The predictive value of water
models has been questioned [202]
and, even with current developments, their general application
should be approached with caution [203].
Clearly the water molecule is a flexible molecule with electronic
polarization and models that do not include both these characteristics
together with their interactions are unlikely to be good predictors. 
The agreement of the icosahedral
cluster model of water with the O···O
radial distribution function is in marked contrast to
the use of many polarizable and non-polarizable models
for water, which do not show any fine
structure. The popular TIP4P model underestimates the tetrahedrality of the water molecule's environment, which explains its poor
estimate of the dielectric constant. It is, however, remarkably
good at qualitatively describing water's phase diagram [669]
and this has been developed further in TIP4P/Ice [838]. The SPC/E, PPC, and TIP4P,
[3] and BSV, CC, DC, SPC/E and TIP4P,
[93] models are reported
as failing to properly describe the experimental O···O
radial distribution function. The TIP3P and SPC show particularly poor agreement, the TIP4P, SPC/E and PPC show improved agreement but the recent models TIP4P-FQ and increasingly used TIP5P give further improvement [199]
at a computational cost. The
popular models SPC, SPC/E, TIP3P and TIP4P produce poor agreement with water's melting point (giving
melting points of 190 K, 215 K, 146 K and 232 K respectively)
and SPC, SPC/E, TIP3P and TIP5P do not give ice1h as a stable phase,
replacing it with ice II [775] or improbable
unrealistic crystal structures and many models mistakenly predict antiferroelectric character for the ordered phases of ice (e.g. ice XI) [1051]. Different models also
give very different lowest energy structures for small water
clusters [857]. It
is also true that models for liquid water bearing little relationship
to reality (e.g.
involving only two dimensions or 8-molecule cubic arrangements) can be
used to calculate similarly close results for a small number of water's
properties. Nonpolarizable models have been shown to be inherently
unable to simultaneously predict certain physical properties, such as
melting temperature and the temperature of maximum density, whatever
parameter values are chosen due to the limited number of variable
parameters [1079]. None
of 40 rigid, flexible, polarizable and ab initio models were capable of simultaneously agreeing with both the
experimental radial distribution model and the experimental
internal energy [245].
Serious discrepancies, concerning the first coordination shell
hydrogen bonding, have been noted between the molecular dynamics
simulations using these models and X-ray absorption spectroscopy
[613]. Other
modeling studies have failed to reproduce parts of water's
vibrational spectrum even qualitatively [696].
Artifacts, such as phase transitions, may be unexpectedly produced in water simulations [1056] or, worse, go unnoticed. More complete agreement may require many-body parameters [221]
as three-body effects have been shown to contribute 14.5%
(or more [728]) to the internal
energy and these cannot be properly represented by potentials
that distort two-body effects [465].
A recent model (GCPM ) using polarizable smeared charges, rather than the other
models' point charges, has however shown considerable promise
[859]. Other recent steps forward
are the inclusion of quantization, which is shown to have significant
consequences on water's structuring [863],
and the need for high order multipole components, up to hexadecapole,
in order to achieve the correct ferroelectric structures for the
ordered ice phases [1051].
In a study attempting to combine diffraction, infrared and x-ray
absorption data, it was concluded that current water models show poor
fit [1159].
Altogether, it is clear that in spite of water appearing to be a very
simple molecule, it remains very difficult to model realistically.
In the light of these observations, it is unsurprising
that contemporary water models are relatively poor predictors for
the conformation and hydration of biological molecules in
solution (e.g. [596])
and it may be useful to develop water models specifically
for use with biomolecular solvation.
a Note, however that water is
not a spherically symmetrical molecule as judged by the variation
in the van der Waals radii [206]. Also, in these models the
Lennard-Jones interaction exerts a repulsive effect on hydrogen
bonding whereas some report it is attractive [548]
even at this close contact. The Lennard-Jones potential is
made up of a twelfth power repulsive term and a sixth power
attractive term:
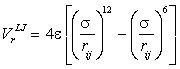
Shown below right is the Lennard-Jones potential
for the SPC/E model (solid red line). The σ parameter gives the molecular separation for zero interaction
energy. The minimum energy (-ε)
lies 12% further at σx21/6 Å.
Also shown (dotted blue line) is an equivalent Buckingham potential (σ 3.55 Å, ε 0.65 kJ mol-1, γ 12.75); the σ parameter in
the Buckingham potential gives the σx21/6 position in the Lennard-Jones potential.
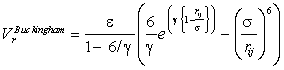 [859] [859]
[Back] |
|
b Models may be
checked for agreement with gas phase clusters (e.g. water dimers) before use in liquid water simulations. Such
compliance, however, should not be a necessary prerequisite
for accurate liquid water predictions. [Back]
c Molecular polarization
may be electronic (caused by the redistribution of its electrons),
geometric (caused by changes in the bond lengths and angles)
and/or orientational (caused by the rotation of the whole
molecule) [867]. This paper [867]
describes Charge-On-Spring polarizable force fields (e.g. COS/G3)
as most suitable for aqueous solutions of proteins. Alternatively,
a model possessing out-of-plane polarization and fluctuating
charges (POL5/TZ)
is proposed best for comparison with experimental vibrational
data [878].
[Back]
d One model describes
the water molecule solely in terms of dipoles and polarizabilities
on the atoms and a quadrupole on the oxygen atom. [736].
[Back]
|