Butane provides a relatively simple demonstration of the energetic issues we face in evaluating rotational isomerism.  Our goal is to understand several things:

  • What will be the most stable conformer of an alkane (or other molecule?
  • What general principles can we find in order to make a prediction for a molecule we've never seen?
  • What are the underlying physical laws that control energy vs. conformation?
  • How should we think about what a collection of molecules will "look like"?
The analysis requires is to define a measure of physical structure.  We will use the dihedral angle, the angular measure of the "twist" of groups around a bond.  In this analysis, we are looking at the dihedral angle between the two terminal methyl groups in butane.

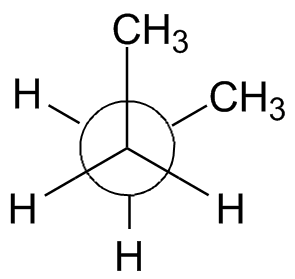
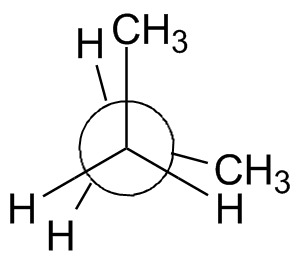
A very useful drawing convention is the Newman projection, named after the chemist who invented it in the 1960s.  To draw a Newman projection, use the following process:
  1. Draw a circle.  This represents the bond down which we look.
  2. If the front carbon is sp3-hybridized, draw three lines that meet at the center of the circle, 120° apart.  (An sp2 carbon will use 2 lines 180° apart)
  3. If the back carbon is sp3-hybridized, draw three lines outside the circle that stop at the circle's edge.  These three will be 120° apart; the angular separation between a front-atom bond and a rear-atom bond is the dihedral angle.

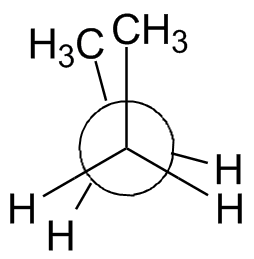
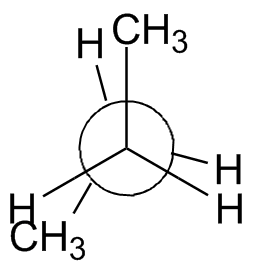
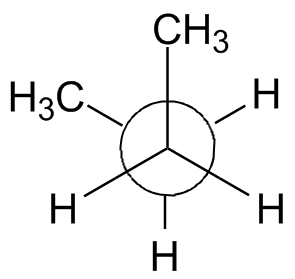
The rotation about the center bond in butane is shown in the chart below using 3-D Jmol structures.  You should build a model.  Compare to Figure 2-13 in the text and the Newman projections shown.
Syn: Butane 0°
Gauche: Butane 60°
Eclipsed: Butane 120°
Anti: Butane 180°
Eclipsed: Butane 240°
Gauche: Butane 300°
Syn: Butane 360°
Butane Newman Projection
Newman projection: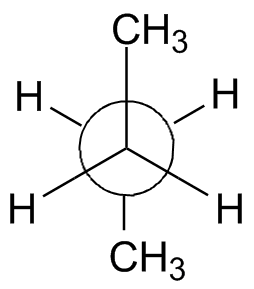

Staggered-anti
Eclipsed
Staggered-gauche
Eclipsed-syn
Staggered-gauche
Eclipsed
Staggered-anti
Staggered, anti, 180°
 Eclipsed, 240°
 Staggered, gauche, 300°
 Eclipsed, syn, 360°
 Staggered, gauche, 60°
 Eclipsed, 120°
 Staggered, anti, 180°
Energy: 0
 Energy: +3.6 kcal/mol
(+16 kJ/mol)
 Energy: +0.9 kcal/mol
(+3.8 kJ/mol)
 Energy: +5 kcal/mol
(+19 kJ/mol)
 Energy: +0.9 kcal/mol
(+3.8 kJ/mol)
 Energy: +3.6 kcal/mol
(+16 kJ/mol)
An understanding of the source of the higher energies can be seen with space-filling models. The space-filling model attempts to convey the location of the electron cloud around each atom.  We see that the high energies come from moving electron clouds close together.  The closer they get, the higher the energy.  Generally:
  • Staggered conformations are more stable than eclipsed
  • Anti conformations are most stable; each gauche interaction costs about 0.9 kcal/mol.
From examination of ethane, we know that a CH-CH eclipsing interaction costs 0.9 kcal/mol.  We can deduce, then, that each CH-CC eclipsing interaction costs (3.6 kcal/mol - 0.9 kcal/mol)/2 = 1.4 kcal/mol.  A CC-CC eclipsing interaction costs (5.0 kcal/mol - 2 x 0.9 kcal/mol) = 3.2 kcal/mol.

The energies tell us how much of any form will be present in a collection of the molecules.  Remember the equation for equilibrium:

ΔG° = -RTlnKeq

The equilibrium between anti and gauche is a function of the energy difference (0.9 kcal/mol) and comes out to be Keq = 4.57 at room temperature.  This works out to a mixture that is 82% anti, 18% gauche.  (Work out the K for the eclipsed conformations, and you will find there will be <0.1% of either.)