Waves on a String, Waves on a Caternary

This assignment was to investigate waves of the following formula:

where:

For all of the below cases, this is the code that I used.  I wrote it to be very general.  A switch statement is used to change which initial condition is used.  I also have all of the different forms of the differential equation to be solved in it.  All that needs to be done is uncomment one and comment the others to go between the different cases.

Also in my code, is a set of commands that create the batch file used by gnuplot to make the animations.  This set of commands in gnuplot by itself does not actually make the animation, only the frames for it.  To make the animation from these pictures, all that is required is to issue the linux command :
convert *.png animation.gif
in the directory containing the pictures.  Note that the png files must be in numerical order, or else the animation will not be in the correct order.

I first started with the simple case of a wave on a string with no friction or gravity. I did this for a couple of different cases.

First I used a single pluck:

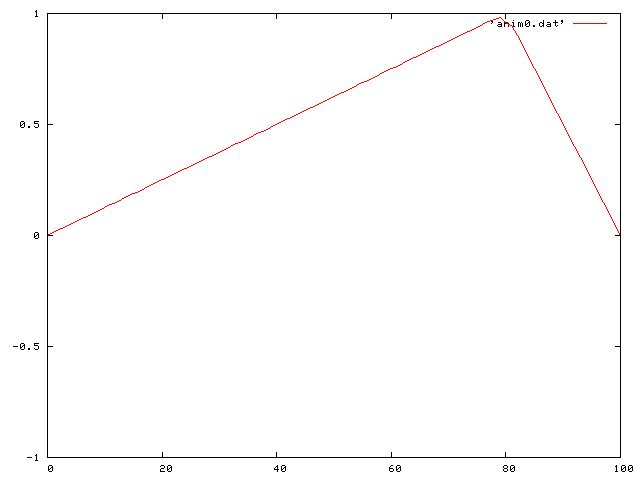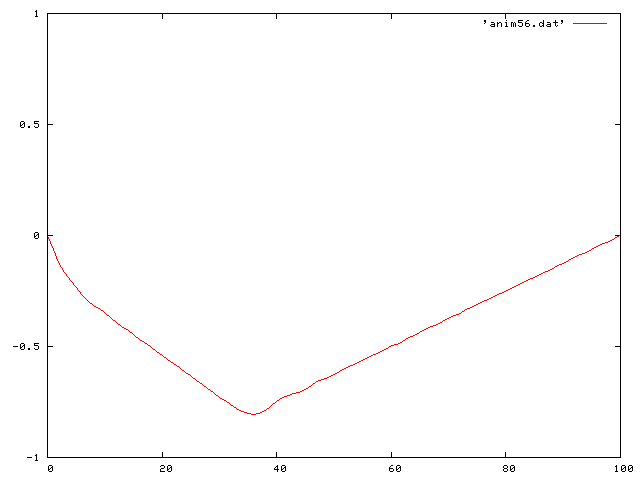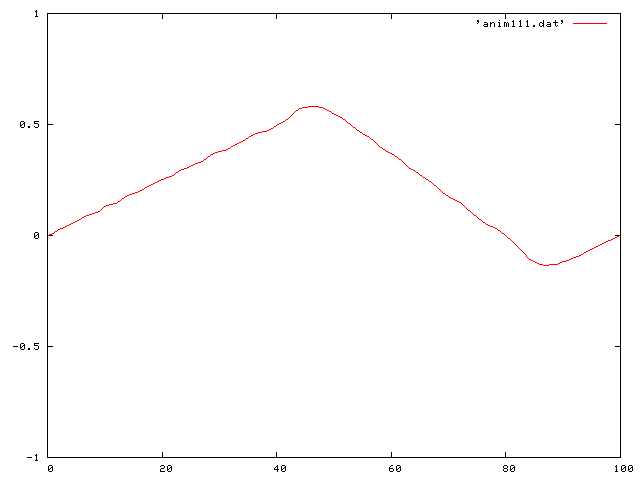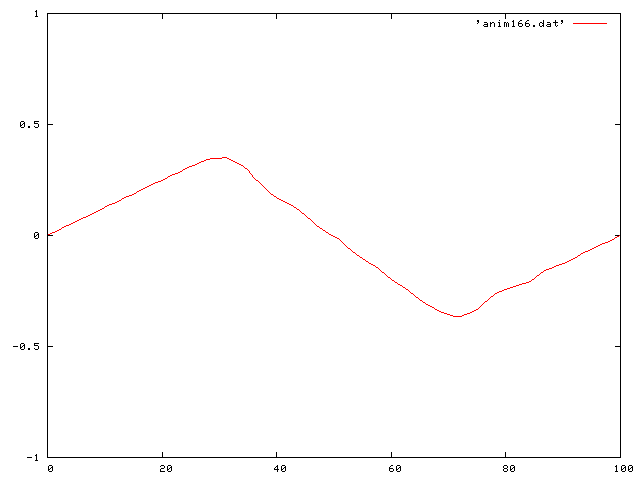
Then a double pluck:

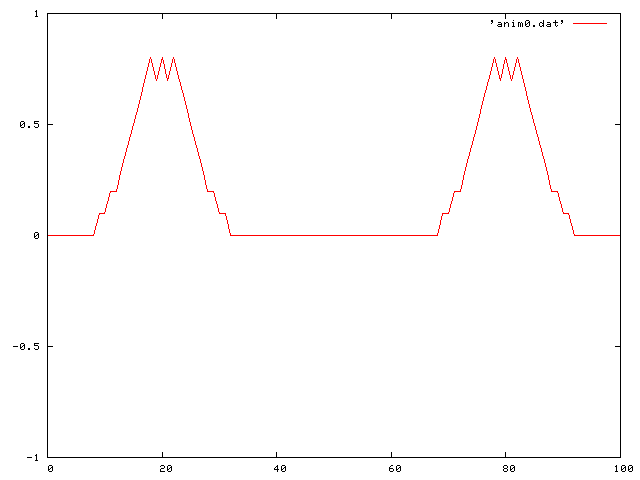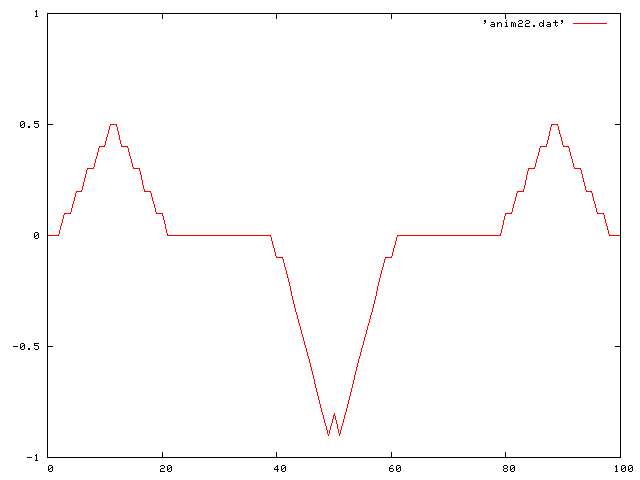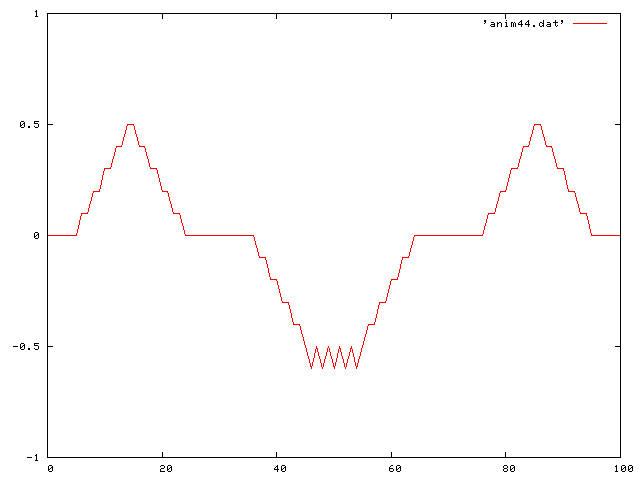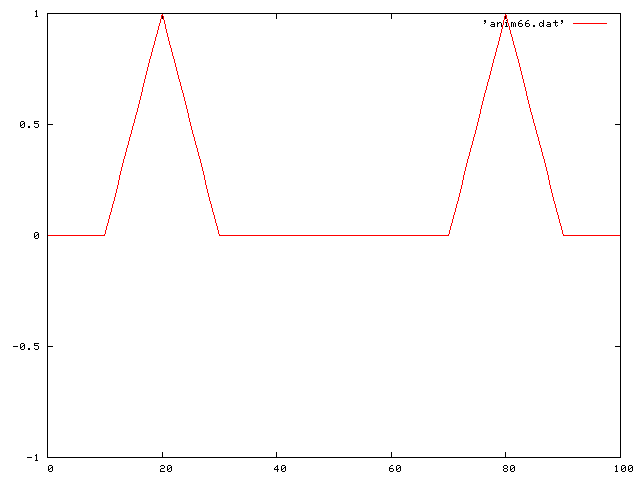
Then a standing sine wave:

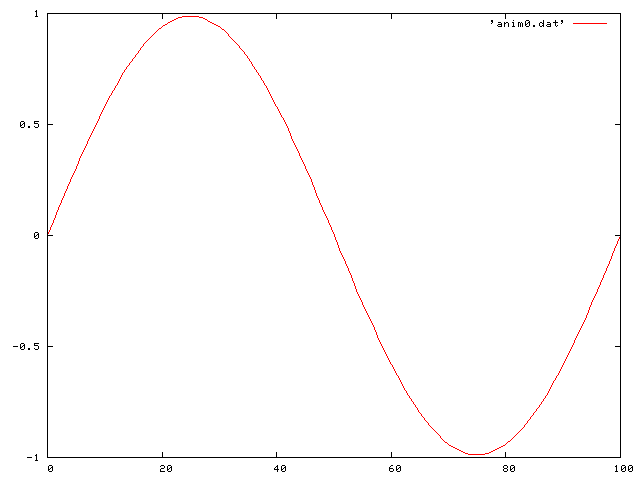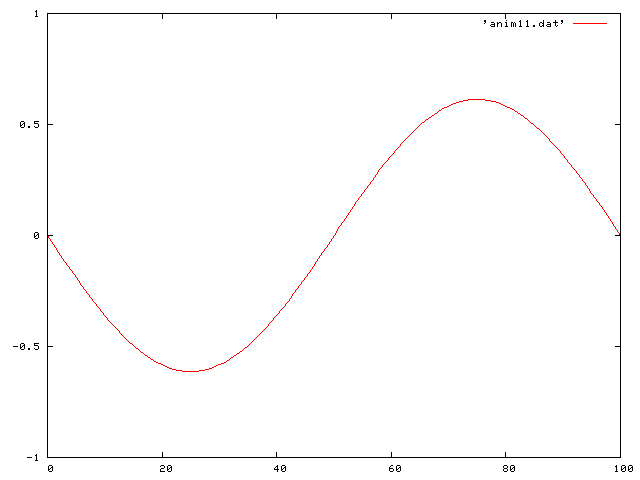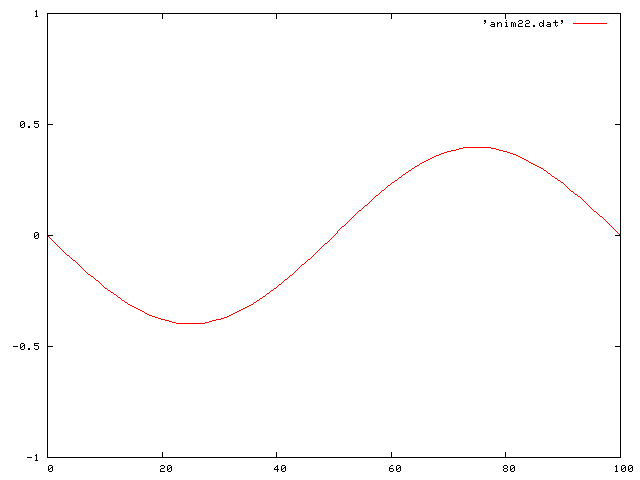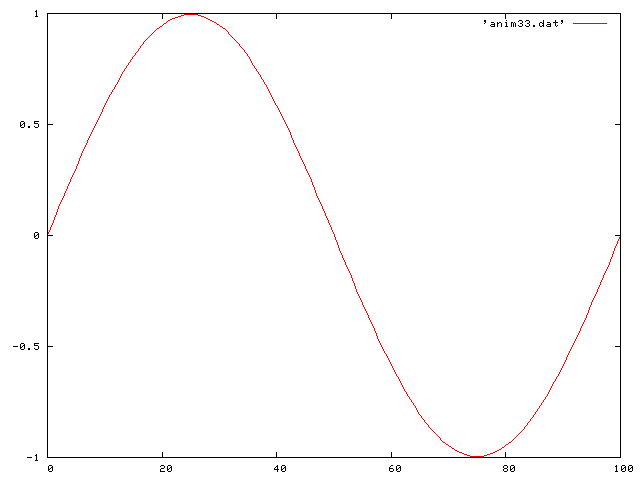
Then a half sine wave:

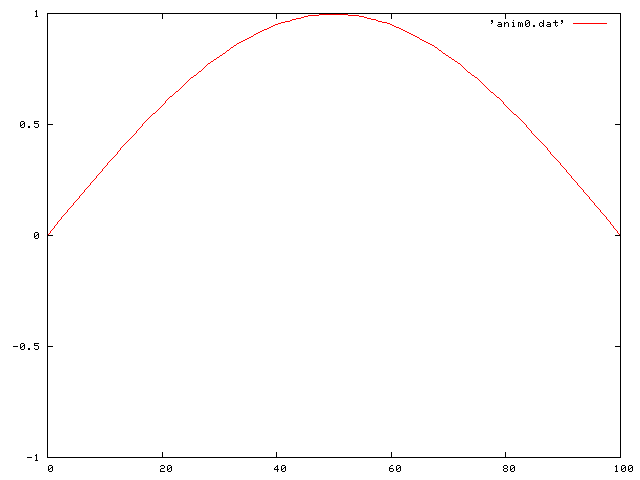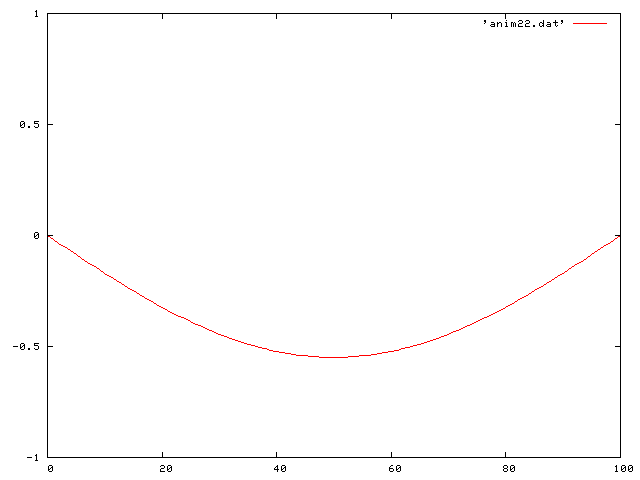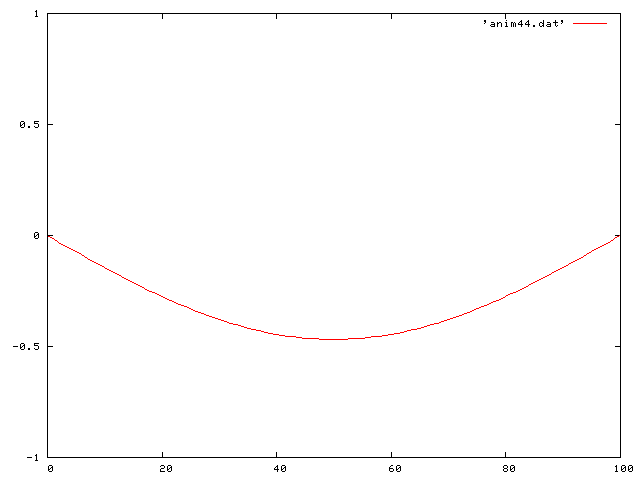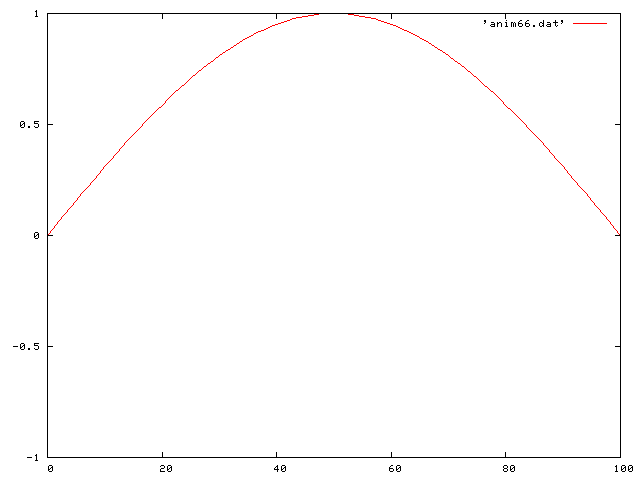
I next looked at the case where friction is added. The differential equation than becomes:

where κ is the coefficient of friction. Here I only looked at the case of the single pluck.

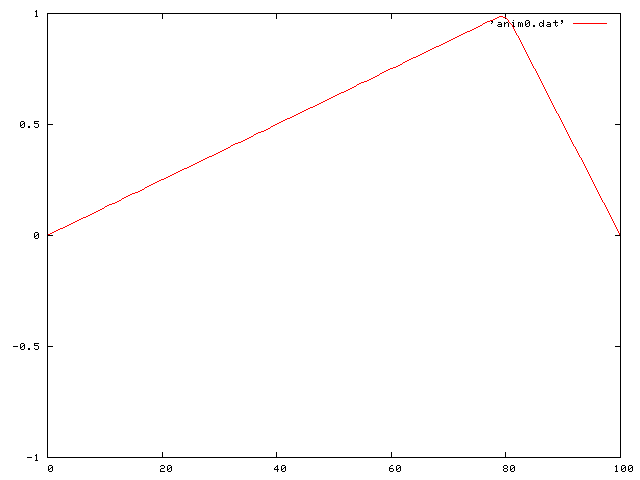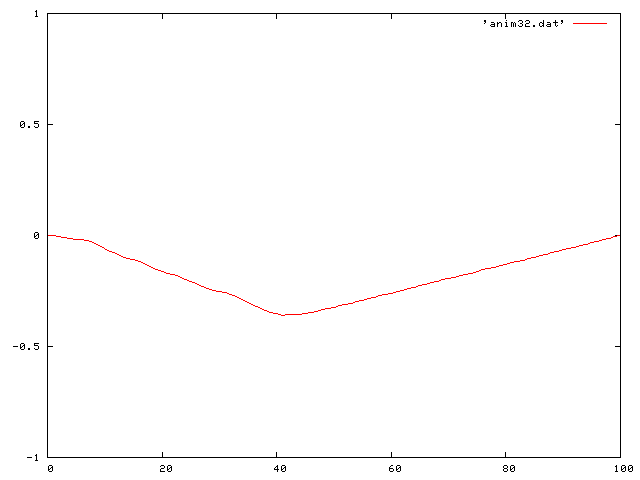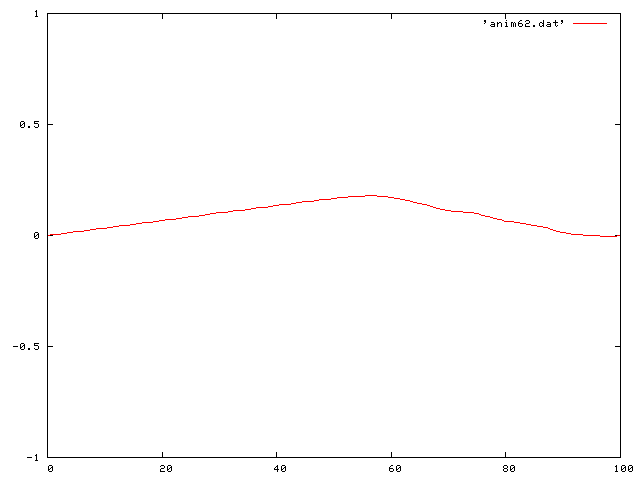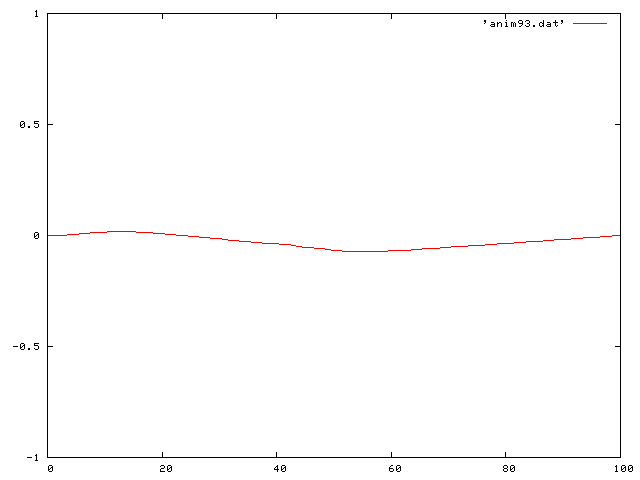
Note how the wave is decreasing in time. I also looked at the case of the single pluck, but where the coefficient of friction is negative. In this case the wave increases in size. This case is unphysical and violates our condition of small oscillations.

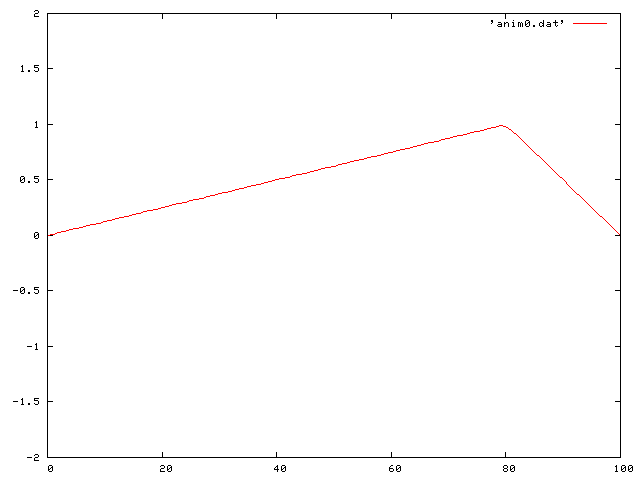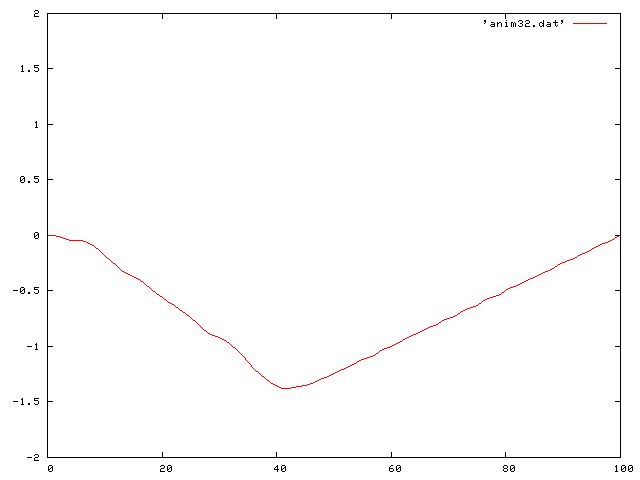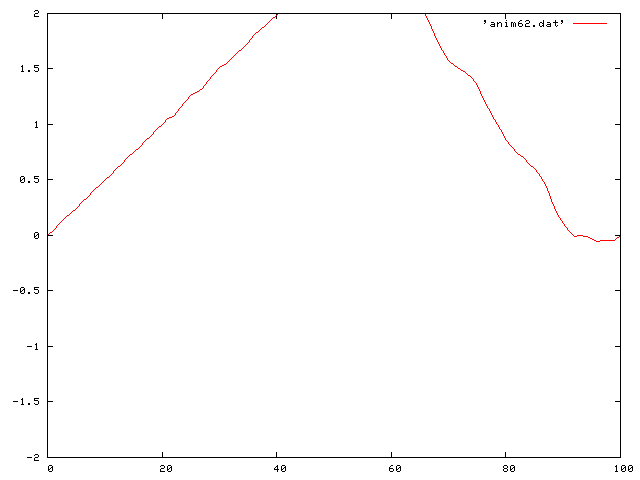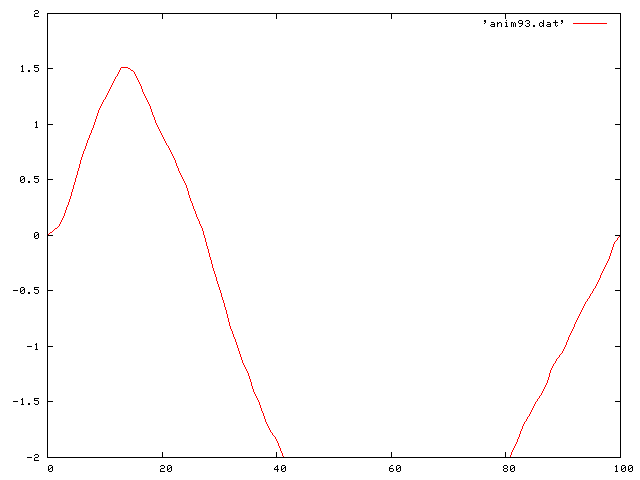
Now I look at the really interesting cases. That is, including gravity. I first looked at the case of no friction. The differential equation then becomes:

where:

and

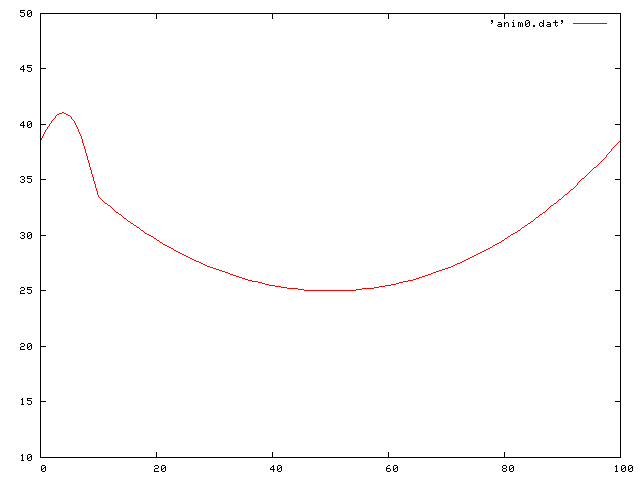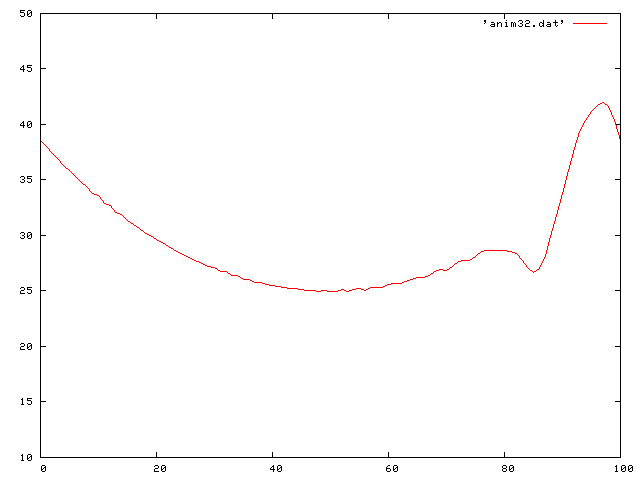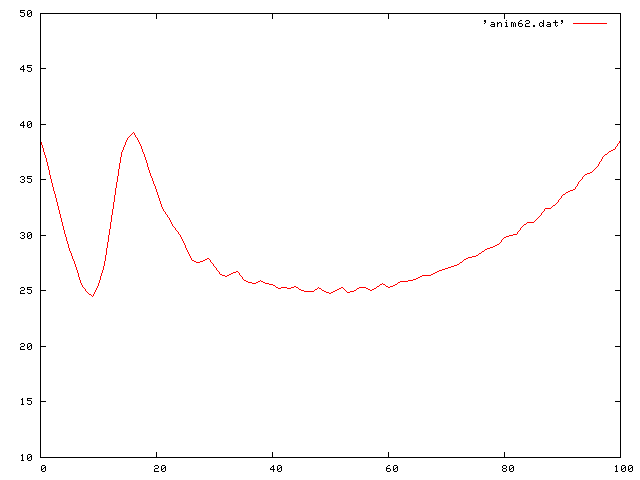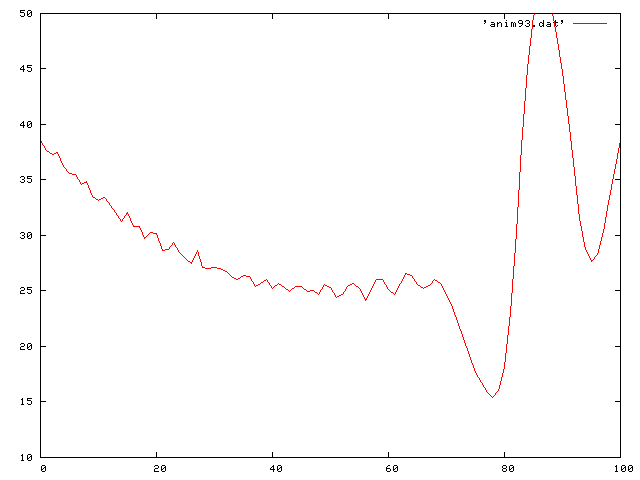
Here is the case of the initial configuration being that of a cosh function offset from the relaxed position:

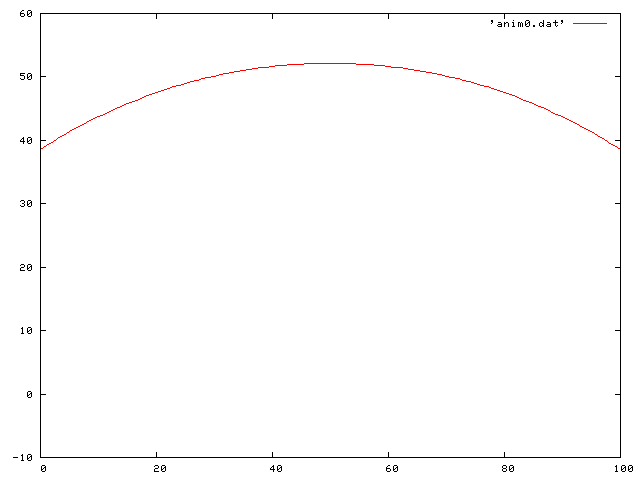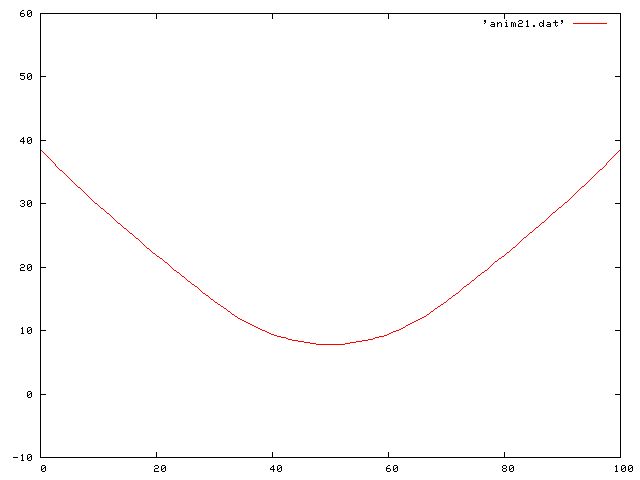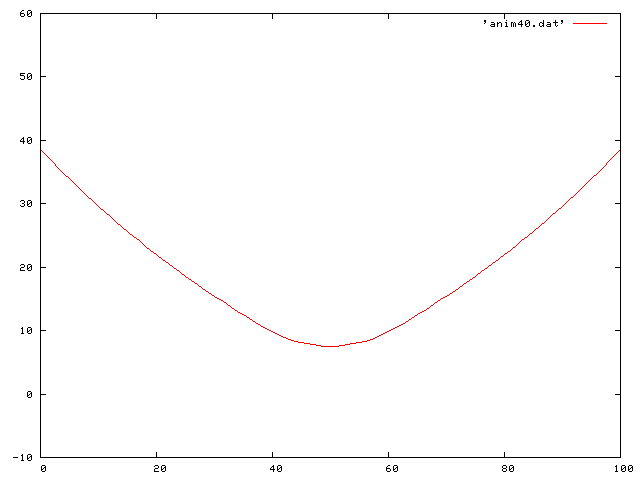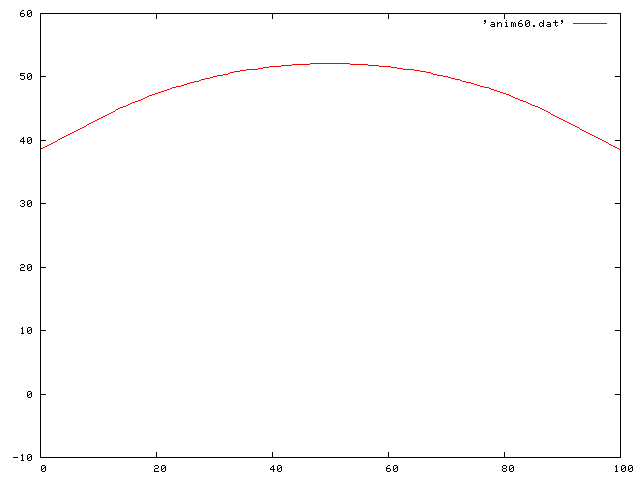
Here is a traveling sine wave along the string:

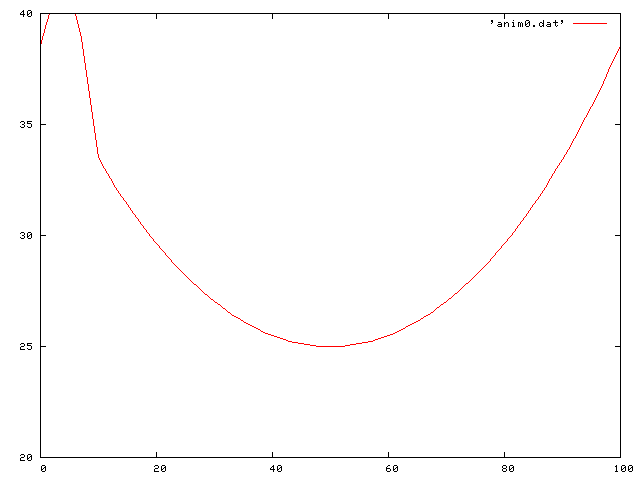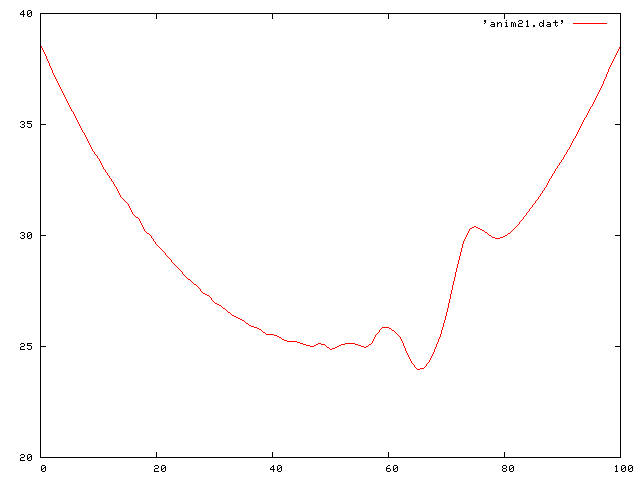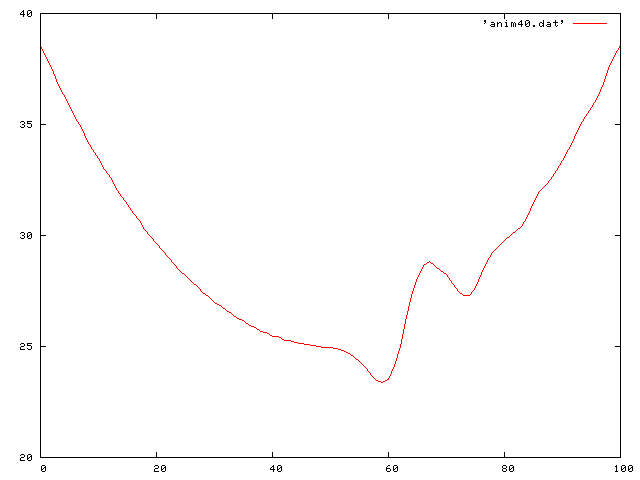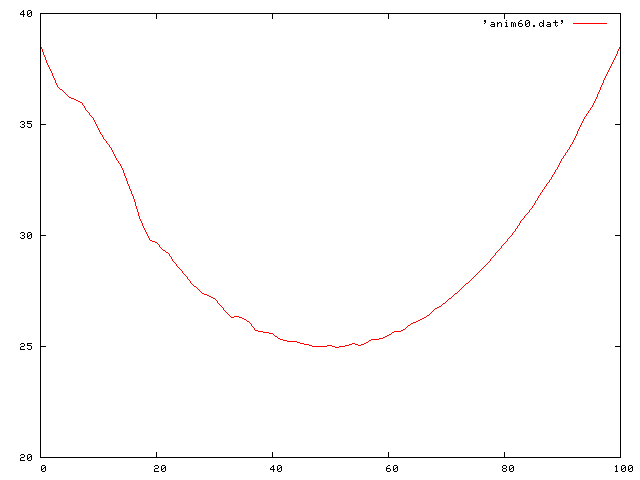
Now I put it all together and look at the case of gravity and friction. The differential equation then becomes:

Here we see a traveling decreasing sine wave along the string:

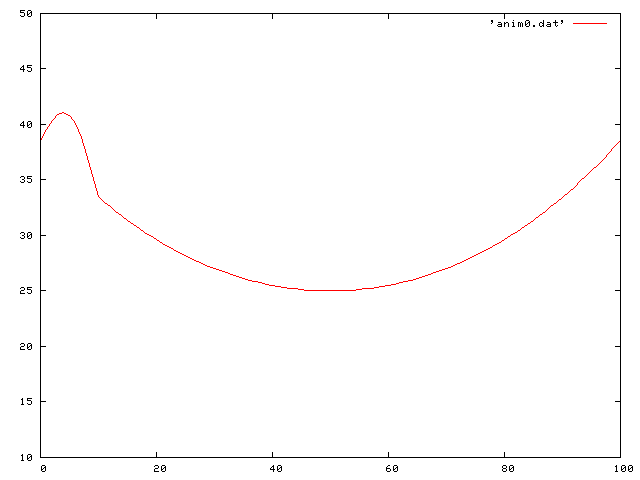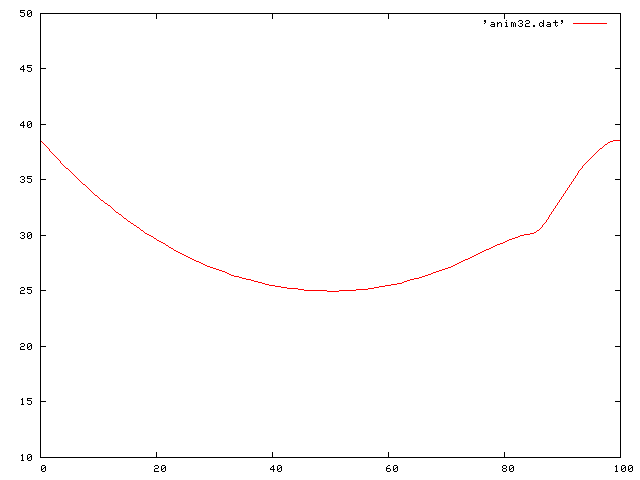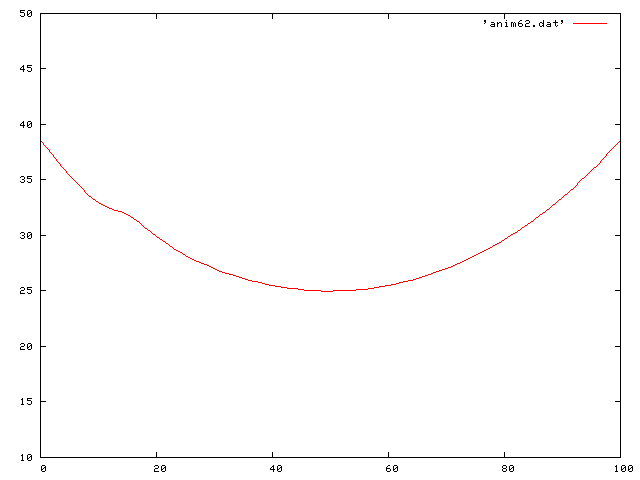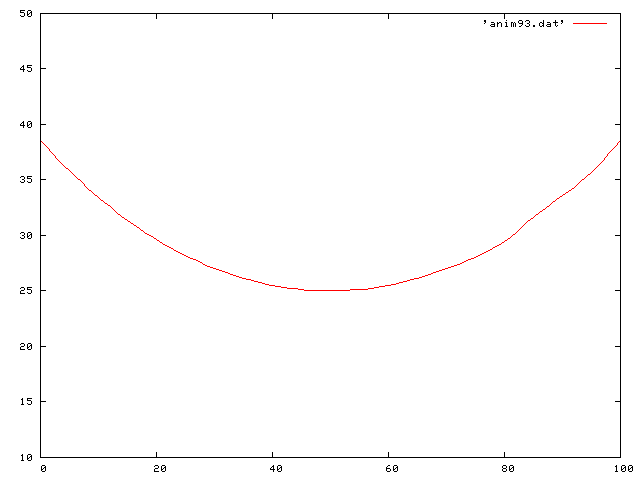
Here is the same traveling sine wave, but with a negative coefficient of friction so that it increases in time: