- §1. Differential Forms
- §2. Higher Rank Forms
- §3. Polar Coordinates
- §4. Linear Maps
- §5. Cross Product
- §6. Dot Product
- §7. Products of Forms
- §8. Pictures of Forms
- §9. Tensors
- §10. Inner Products
- §11. Polar Coordinates II
Pictures of Differential Forms
How do vectors act on functions? By telling you how much the function changes in the direction of the vector. This action is given by \begin{equation} \vv(f) = \vv\cdot\grad f \label{vact} \end{equation} and involves differentiation. But we have also seen that the 1-form $df$ corresponds to $\grad f$, through the Master Formula ($df = \grad f\cdot d\rr$) and we can therefore regard (\ref{vact}) as an action of the 1-form $df$ on the vector $\vv$, given by \begin{equation} df(\vv) = \vv(f) = \grad f\cdot\vv \end{equation} This action does not involve differentiation, but only linear algebra, and therefore lends itself to a geometric interpretation in terms of stacks. 1)
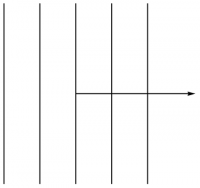
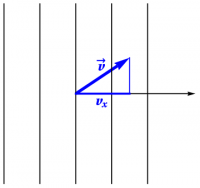
Consider first the 1-form $dx$. From calculus, we know that $dx=0$ along surfaces of the form $x=\hbox{constant}$. What does $dx(\vv)$ represent? We have $dx=\grad x\cdot d\rr=\xhat\cdot d\rr$, so $dx(\vv) = \xhat\cdot\vv = v_x$ is just the $x$-component of $\vv$. How can we display this information visually?
We represent $dx$ as an oriented stack of surfaces $x=\hbox{constant}$. Since we have associated $dx$ with $\xhat$, we choose unit spacing between the surfaces. Thus, $dx$ corresponds to the drawing in Figure 1, where the arrow gives the orientation, namely the direction in which $x$ is increasing. To evaluate $dx(\vv)$, all we need to do is superimpose $\vv$ on this stack, as shown in Figure 2, then count how many surfaces $\vv$ goes through, which in this case is $\frac32$. If the stack had been oriented the other way (corresponding to $-dx$), then the answer would have been negative.
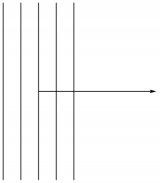
Now that we know how to represent $dx$, how can we represent $2\,dx$? Clearly, the result of acting on a vector with $2\,dx$ should be twice that of acting on it with $dx$. But the vector doesn't change, so it must go through more surfaces. Thus, $2\,dx$ is represented by the same drawing as in Figure 1, but with the spacing between the surfaces reduced by a factor of two, as shown in Figure 3. This construction should remind you of a topographic map, where the contour lines are closer together the steeper the terrain is.
How do we add stacks? Remarkably, the process is simple: simply superimpose the corresponding stacks, and connect points of intersection. This construction is shown in Figure 4 for the addition of $dx$ and $dy$. It is straightforward but somewhat tedious to verify that this procedure yields the correct spacing between surfaces, which is $\frac{1}{\sqrt{a^2+b^2}}$ for $a\,dx+b\,dy$. (Why?)
The description of stacks given above works fine for constant 1-forms, but not for 1-form fields. Just as a vector field is a vector at each point, a 1-form field is a 1-form at each point. Thus, to represent a 1-form field, we need a stack at each point.
For example, Figure 5 shows the stacks corresponding to $r\,dr=x\,dx+y\,dy$, and Figure 6 shows the stacks corresponding to $r^2\,d\phi=-y\,dx+x\,dy$. Since $r\,dr=\frac12\,d(r^2)$, the first example could have been represented by a topographic map whose contours are circles; this 1-form corresponds to the conservative vector field $r\,\rhat=x\,\xhat+y\,\yhat$. However, the vector field $-y\,\xhat+x\,\yhat$ is not conservative; the second example does not correspond to any topographic map. Stacks provide a useful geometric representation in both cases, but they do not in general combine to form a global representation in terms of contours. 2)
Similar methods can be used to represent higher-order forms. For example, the 2-form $dx\wedge dy$ is shown in Figure 7. The 2-form $dx\wedge dy$ acts on pairs of vectors $(\uu,\vv)$. How? Construct the parallelogram whose sides are $\uu$ and $\vv$, then superimpose it on the drawing; the number of “cells” covered by the parallelogram gives the result of $dx\wedge dy$ acting on ($\uu,\vv$), with the overall sign determined by the relative orientations. Again, this drawing shows a constant 2-form, a general 2-form (field) would be represented by a similar drawing at each point.
Similar constructions apply in higher dimensions. 3)