Vector Fields

The best way to introduce vector fields is with an example. Consider the two-dimensional vector field

For each point (x,y) in the xy-plane the function F(x,y) assigns a vector. The coefficient of i is the x component of the vector. The coefficient of j is the y component of the vector. Alternatively, we can use the notation <y,sin x> to denote the vector field. The figure below plots the vector field.

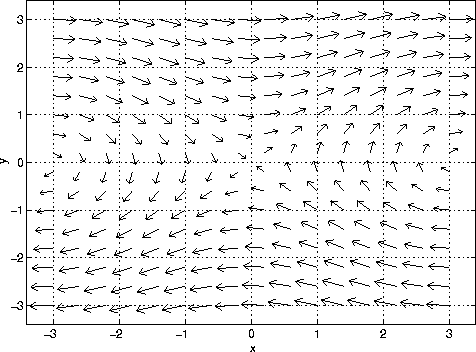
The length of the vector in the plot is proportional to the actual magnitude of the vector.

In general, a vector field in two dimenensions is a function that assigns to each point (x,y) of the xy-plane a two-dimensional vector F(x,y). The standard notation is

Here P(x,y) is the x-component function of the vector field and Q(x,y) is the y-component function of the vector field. In some cases the vector field is only defined for a region D of the xy-plane.

A vector field in three dimensions is a function F that assigns to each point (x,y,z) in xyz-space a three dimensional vector F(x,y,z). The notation is

Again, the vector field may only be defined in a certain region D of xyz-space.

Vector fields arise in a number of disciplines in the physical sciences including

Mechanics: gravitational fields. At each point the vector field gives the direction and magnitude of the force on a particle.
Electricity and Magnetism: electric and magnetic fields. At each point the vector field gives the direction and magnitude of the force on a particle.
Fluid Mechanics: velocity fields. At each point the vector field gives the velocity of a fluid.

Conservative Vector Fields

A type of vector field arising in a number of applications, including mechanics and electricity and magnetism, is a conservative vector field. In this case the vector field is defined in terms of the gradient of a scalar function f(x,y,z):

Vector Fields versus Vector Functions

Vector fields and vector functions are two different types of functions. Recall that a vector function in three dimensions is denoted r(t)=<f(t),g(t),h(t)>. A vector function has three components, each of which is a function of ONE variable. A vector function represents a curve in space.

A vector field in three dimensions, F(x,y,z)=<f(x,y,z),g(x,y,z),h(x,y,z)>, has three components, each of which is a function of THREE variables. A vector field assigns a vector to each point in a region in xyz space.

[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]

If you have questions or comments, don't hestitate to contact us.