Divergence of a Vector Field
The divergence of a vector field F=<P(x,y,z),Q(x,y,z),R(x,y,z)>, denoted by div F, is the scalar function defined by the dot product
![]()
Here is an example. Let
![]()
The divergence is given by:
![]()
Curl of a Vector Field
The curl of a vector field F=<P(x,y,z),Q(x,y,z),R(x,y,z)>, denoted curlF, is the vector field defined by the cross product
![]()
An alternative notation is
![]()
The above formula for the curl is difficult to remember. An alternative formula for the curl is
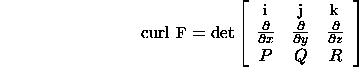
det means the determinant of the 3x3 matrix. Recall that the determinant consists of a bunch of terms which are products of terms from each row. The product of the terms on the diagonal is
![]()
As you can see, this term is part of the x-component of the curl.
Consider the following example: F=<xyz,ysin z, ycos x>.
curl F = <cos x - ycos z, xy + ysin z, -xz>.
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.