For a function of one variable, we can construct the (unique) tangent line to the function at a given point using information from the derivative. The derivative at a point tells us the slope of the tangent line from which we can find the equation of the tangent line:
![]()
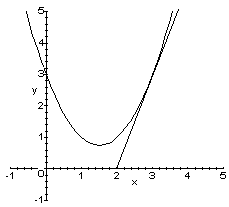
The graph below shows the function y(x)=x^2-3x+3 with the tangent line throught the point (3,3).
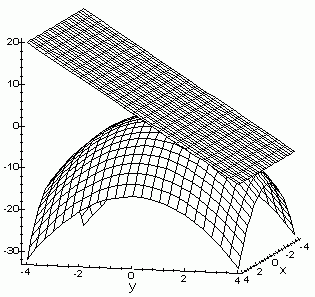
For functions of two variables (a surface), there are many lines tangent to the surface at a given point. If we have a nice enough function, all of these lines form a plane called the tangent plane to the surface at the point. The tangent plane to the surface z=-x^2-y^2 at the point (0,2) is shown below. The logical questions are under what conditions does the tangent plane exist and what is the equation of the tangent plane to a surface at a given point.
Let P_0(x_0,y_0,z_0) be a point on the surface z=f(x,y) where f(x,y) is a differentiable function. The equation of any plane passing through P_0 has the form A(x-x_0)+B(y-y_0)+C(z-z_0)=0. If we divide through by C and set a=-A/C and b=-B/C then we have a(x-x_0)+b(y-y_0)-(z-z_0)=0. If we hold y constant (say y=y_0 for convenience), then we have a curve H=f(x,y_0) passing through P_0 in the surface z=f(x,y) and a line z-z_0=a(x-x_0) passing through P_0 in the plane.
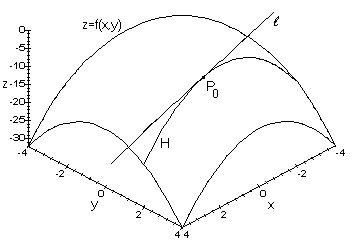
As illustrated by the figure, we want this line in the plane to be tangent to the surface z=f(x,y) at P_0 and thus tangent to the curve in the surface. This means we want the number a to be the slope of the tangent line to the curve H=f(x,y_0). This slope is by definition the partial derivative of f with respect to x at (x_0,y_0). Hence, a=f_x(x_0,y_0). By holding x constant, we can similarly show b=f_y(x_0,y_0). Therefore, the equation of the plane tangent to the surface z=f(x,y) at the point P_0(x_0,y_0,z_0) is
![]()
Notice the similarity between the formula for the tangent line given in the introduction and the formula for the tangent plane. We can easily identify the normal vector to the plane:
![]()
This vector is also then normal to the surface z=f(x,y) at the point P_0(x_0,y_0,z_0).
To find the equation of the tangent plane to the surface z=2x^2-xy^3 at the point (1,2), we first need to find the partials of z with respect to x and y at (1,2):
![]()
Then, a normal vector to the surface at (1,2) is <-4,-12,-1> which implies the equation of the tangent plane to the surface at (1,2) is -4(x-1)-12(y-2)-(z+6)=0 or equivalently 4x+12y+z=22.
Given a function y=f(x) and a point (c,f(c)) on the curve, the quantity
![]()
is the change in y along the curve y=f(x) produced by a change (delta)x in x. The differential dy=f '(x)dx is the change in y along the tangent line at c produced by a change dx in x. The differential closely approximates (delta)y for small (delta)x=dx (see the figure below) and is much easier to compute. We seek a similar approximation for functions of two variables.
For a function z=f(x,y) the quantity
![]()
is the change in z along the surface z=f(x,y) produced by small changes (delta)x and (delta)y in x and y, respectively. To find a corresponding formula for dz, consider a point P_0(x_0,y_0,z_0) on the surface with tangent plane
![]()
This equation implies the surface has height z_0 at (x_0,y_0) and height
![]()
when x_0 and y_0 are changed by dx and dy, respectively. Thus, the change in the height of the tangent plane is
![]()
This is the total differential of z=f(x,y) at (x_0,y_0), and it closely approximates the functional change (delta)z for small (delta)x=dx and (delta)y=dy.
The total differential of the function z=ln(xy)+x^2+y is
![]()
If x changes from 1 to 1.05 and y changes from 2 to 1.98, then the values of dz and (delta)z are
![]()
![]()
[Vector Calculus Home] [Math 254 Home] [Math 255 Home] [Notation] [References]
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.