This page contains the following sections:
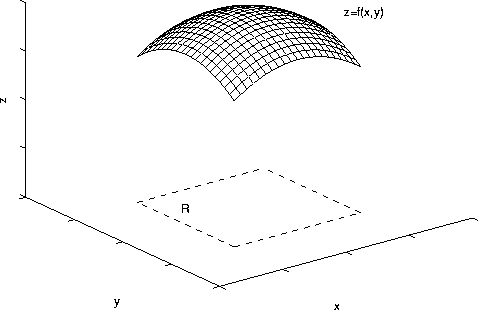
Let z=f(x,y) define a surface in xyz space above a region R in the xy plane. Suppose that the density per unit area of the surface is given by the function P(x,y,z). What is the mass of the surface?

Consider a patch of the surface above an infinitesimal region in the xy plane around the point (x,y) with area dA. It can be shown that the surface area of this patch of the surface is
![]()
Hence, the mass of the surface is (density times area) is
![]()
In this last formula we have used the facts that z=f(x,y) and that the density P(x,y,z) is essentially constant on the small patch of surface. The total mass is the sum of the masses of the patches of surface above all infinitesimal regions in R:
![]()
This is a double integral.
The notation for a surface integral of a function P(x,y,z) on a surface S is
![]()
Note that if P(x,y,z)=1, then the above surface integral is equal to the surface area of S.
Compute the surface integral
![]()
where S is that part of the plane x+y+z=2 in the first octant. A plot of S is given below.
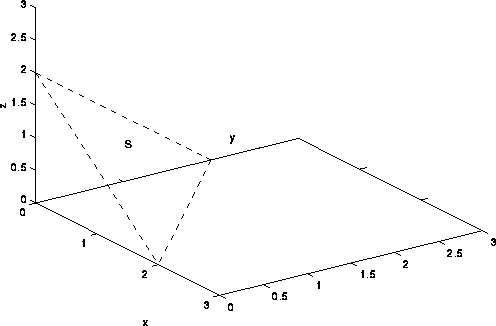
Rewriting the equation of the plane in terms of z, we have z=f(x,y)=2-x-y. In this case, we have f_x=-1, f_y=-1 Hence the integral becomes:
![]()
The region R is the triangular region in the figure below:
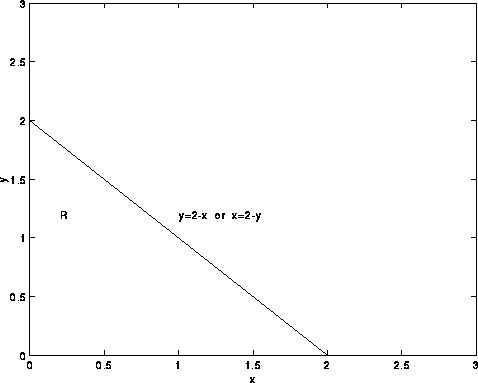
It follows that the double integral can be written
![]()
where c=sqrt(3). (It is also possible to integrate with respect to x first.) Computing the inner integral, we get (remember x is treated as a constant)
![]()
Here we ignore the constant c (it can be pulled out of the integral). Evaluating this last expression, we get
![]()
The outer integral is
![]()
The final answer is 2*c=2*sqrt(3).
Surface Integrals of Surfaces Defined in Parametric Form
Suppose that the surface S is defined in the parametric form
![]()
where (u,v) lies in a region R in the uv plane. In this case the surface integral is given by
![]()
Here
![]()
The x means cross product. A derivation of this formula can be found in textbooks.
Find the mass of the cone below (centered at the origin with base radius 2 and height 3), if the density satisfies
![]()
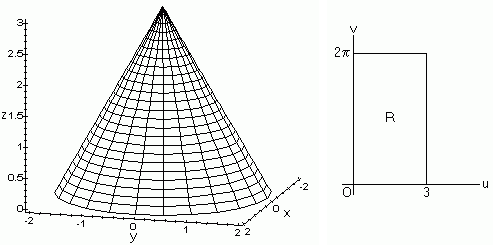
A parameterization of the cone is
![]()
where (u,v) lies in the rectangle in the uv plane shown above. In this case, r_u (the partial derivative of the vector with respect to u) is
![]()
and the partial derivative wrt v is
![]()
Taking the cross product, we have
![]()
The norm of this vector is
![]()
The function P(x,y,z) can be expressed in terms of u and v as well by substituting for x and y. We have
![]()
Hence, the mass is given by
![]()
where C=sqrt(13/9). The integral can be expressed as an iterated integral in u and v:
![]()
The integral is independent of the order of integration. Evaluating the integral, we have
![]()
Copyright © 1996 Department of Mathematics, Oregon State University
If you have questions or comments, don't hestitate to contact us.