Try to isolate the part of the term raised to the n power from the part of the series not raised to the n power. Consider splitting the series into two pieces based on this, if necessary.
So, the sum of 3*(1/2^n) is 3 times the sum of 1/2^n. The sum of 1/2^n converges, so 3 times is also converges. Similarly, the sum of 3+1/2^n equals the sum of 3 + the sum of 1/2^n. Since the sum of 3 diverges, and the sum of 1/2^n converges, the series diverges. You have to be careful here, though: if you get a sum of two diverging series, occasionally they will cancel each other out and the result will converge.
If the power is n+1 or such, then factor out terms until you just have an n power. Then try to match up the term with the Geometric Series: use the part raised to the n power as r, and the part not raised to the n power as a. If it doesn't fit exactly, see if you can use a Comparison Test or Limit Comparison Test.
For instance,
![]()
the sum of which converges to 4/3*(1/(1-2/3)) = 4.
It also may be worthwhile to try the Root Test, since taking an nth root will conveniently rid the term of an nth power. Also, you will often get a lot of cancellation using the Ratio Test.
As an example, look at the sum of (1/3)^(n+2). Using the Ratio Test, we get
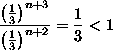
so the series converges.
If you have questions or comments, don't hestitate to contact us.