Error Bounds using Taylor Polynomials

One of the major uses for Taylor Polynomials is using them as approximations for other, transcendental, functions. Another use is for approximating values for definite integrals, especially when the exact antiderivative of the function cannot be found. Here is a list of the three examples used here, if you wish to jump straight into one of them.

We cannot find the value of exp(x) directly, except for a very few values of x. However, we can create a table of values using Taylor polynomials as approximations:

f(x) = exp(x) = f'(x) = f''(x) = f'''(x) =

f^(4)(x) = f^(5)(x) = f^(6)(x).

f(0) = exp(0) = 1 = f'(0) = f''(0) =

f'''(0) = f^(4)(0) = f^(5)(0).

f(x) = T[5](x) + R[5](x) =

1 + x + (x^2)/2 + (x^3)/6 + (x^4)/24 + (x^5)/120 + (exp(z)*x^6)/720

f(x) - T[5](x) = R[5](x) = (exp(z)*x^6)/720

for some z in [0,x]. If x is sufficiently small, this gives a decent error bound. For instance,

the square root of e = e^(1/2) = 1 + 1/2 + 1/8 + 1/48 + 1/384 + 1/3840 + (exp(z))/46080.

So, *** Error Below: it should be 6331/3840 instead of 6331/46080 ***

the square root of e - 6331/46080 = (exp(z))/46080 < 1.7321/46080

since exp(x) is an increasing function, 0 <= z <= x <= 1/2, and

exp(z) <= sqrt(e) < sqrt(3) < 1.7321.

That tells us that *** Error Below: it should be 6331/3840 instead of 6331/46080 ***

sqrt(e) - 6331/46080 < 1.7321/46080 = 0.0000375868...

or *** Error Below: it should be 6331/3840 instead of 6331/46080 ***

sqrt(e) = 6331/46080 which is approximately 1.6487

to at least three decimal places. Taking a larger-degree Taylor Polynomial will make the approximation closer. For instance, the 10th degree polynomial is off by at most (e^z)*x^10/10!, so for sqrt(e), that makes the error less than .5*10^-9, or good to 7decimal places.

Similarly, you can find values of trigonometric functions. Say you wanted to find sin(0.1). Use a Taylor expansion of sin(x) with a close to 0.1 (say, a=0), and find the 5th degree Taylor polynomial.

sin(x) = x - (x^3)/6 + (x^5)/120 + (x^6*cos(z))/720

Since |cos(z)| <= 1, the remainder term can be bounded.

(x^6 * cos(z))/720 <= (x^6)/720

So, for x=0.1,

sin(0.1) is approximately 0.1 - 0.001/6 + 0.00001/120

with an error of at most

0.000001/720,

or sin(0.1) = 0.09983341666... with an error of at most .139*10^-8, or good to seven decimal places.

Let's try a more complicated example. Suppose you needed to find

the integral from 0 to 1/2 of exp(x^2) dx.

Since exp(x^2) doesn't have a nice antiderivative, you can't do the problem directly. Instead, use Taylor polynomials to find a numerical approximation. Let's try a Taylor polynomial of degree 5 with a=0:

f(x) = exp(x^2), f'(x) = 2x*exp(x^2), f''(x) = (2+4x^2)*exp(x^2), f'''(x) = (12x+8x^3)*exp(x^2), f^(4)(x) = (12x+48x^2+16x^4)*exp(x^2), f^(5)(x) = (120x+160x^3+32x^5)*exp(x^2), f^(6)(x) = (120+720x^2+480x^4+64x^6)*exp(x^2)

f(0)=1, f'(0)=0, f''(0)=2, f'''(0)=0, f^(4)(0)=12, f^(5)(0)=0

T[5](x) = 1 + (2x^2)/2 + (12x^4)/24 = 1 + x^2 + (x^4)/2

R[5](x) = (f^(6)(z)*x^6)/720 (where z is between 0 and x)

So,

the integral from 0 to 1/2 of exp(x^2) dx = the integral from 0 to 1/2 of (T[5](x) + R[5](x)) dx =the integral from 0 to 1/2 of T[5](x) dx + the integral from 0 to 1/2 of R[5](x) dx

So,

the integral from 0 to 1/2 of exp(x^2) dx = the integral from 0 to 1/2 of T[5](x) dx

with error

the integral from 0 to 1/2 of R[5](x) dx.

the integral from 0 to 1/2 of T[5](x) dx = the integral from 0 to 1/2 of 1+x^2+(x^4)/2 dx = x + (x^3)/3 + (x^5)/10 from 0 to 1/2 =1/2 + 1/24 + 1/320 = 523/960 = 0.544791666...

The error is

the integral from 0 to 1/2 of R[5](x) dx = the integral from 0 to 1/2 of (x^6 * f^(6)(z))/720 dx

(with z between 0 and x)

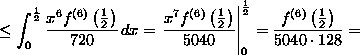
<= the integral from 0 to 1/2 of (x^6*f^(6)(1/2))/720 dx = (x^7*f^(6)(1/2))/5040 from 0 to 1/2 = (f^(6)(1/2))/(5040*128) =

(331*exp(1/4))/645120 which is approximately 0.0006588,

so the answer .54479 is accurate to within .0006588, or at least to two decimal places. Note that the inequality comes from the fact that f^(6)(x) is increasing, and 0 <= z <= x <= 1/2 for all x in [0,1/2].

Copyright © 1996 Department of Mathematics, Oregon State University

If you have questions or comments, don't hestitate to contact us.