Basic calculation I : Silicon¶
Guides you through all necessary steps to create a crystal structure, perform a calculation and generating both bandstructure and density of states (DOS) graphs.
Setup a crystal structure using gem tools¶
Learn or review on how to start gem: First steps with gem.
There are three basic ways to create a crystal structure in gem. We start with the simplest and explain the built in visualization. The other, more general methods of creating a crystal structure are described at the end of this section.
gem knows a few very common crystal structures by their common name. The crystal structure of silicon is called the diamond structure and you can create a silicon structure using the diamond function:
In [1]: s=diamond(a0=5.4,atom1='Si')
In gem a0 specifies the lattice parameter. The structure, the result of the function diamond(), is stored in the variable s. Print it to see its contents:
In [1]: s=diamond(a0=5.4,atom1='Si')
In [2]: print s
diamond
lattice vector 0 = [ 0. 2.7 2.7]
lattice vector 1 = [ 2.7 0. 2.7]
lattice vector 2 = [ 2.7 2.7 0. ]
unitcell volume : 39.366 Ang^3
2 atoms in unitcell
atom 0 : Si [ 0.125 0.125 0.125]
atom 1 : Si [-0.125 -0.125 -0.125]
In [3]:
Two Si atoms but the title says diamond. Let’s fix that:
In [3]: s.title='silicon'
In [4]: print s
silicon
lattice vector 0 = [ 0. 2.7 2.7]
lattice vector 1 = [ 2.7 0. 2.7]
lattice vector 2 = [ 2.7 2.7 0. ]
unitcell volume : 39.366 Ang^3
2 atoms in unitcell
atom 0 : Si [ 0.125 0.125 0.125]
atom 1 : Si [-0.125 -0.125 -0.125]
In [5]:
Not convinced? Let’s create an image. The first command creates an image, which is stored in variable v. The second command adds labels to the atoms:
In [5]: v=s.vis()
In [6]: v.atom_labels.show()
In [7]:
In a separate window, you’ll see
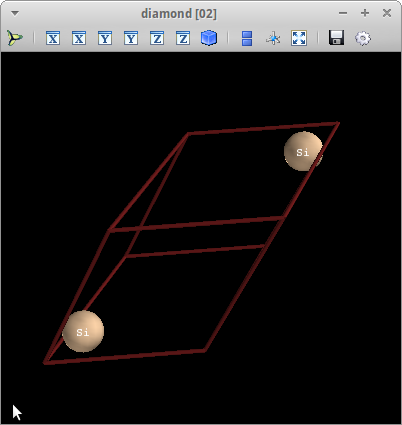
The 3D visualization module used in gem is based on mayavi2, a powerful 3D scientific visualization tool. Using the mouse you can rotate, zoom, and pan the structure. Buttons let you save the image, change background colors etc. See the mayavi2 documentation for more details.
The primitive unit cell doesn’t reveal much about the structure of silicon. Let’s create the conventional unit cell of silicon:
In [7]: sc=s.convcell()
In [8]: vc=sc.vis()
In [9]: vc.pcell.show()
In [10]:
The last command shows the primitive cell inside the conventional cell:
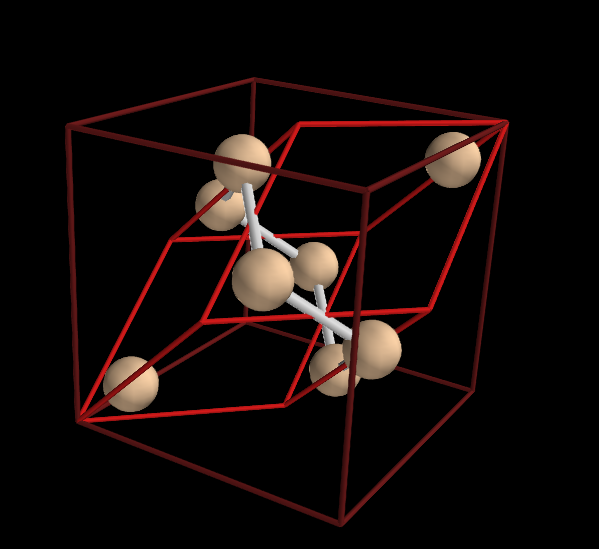
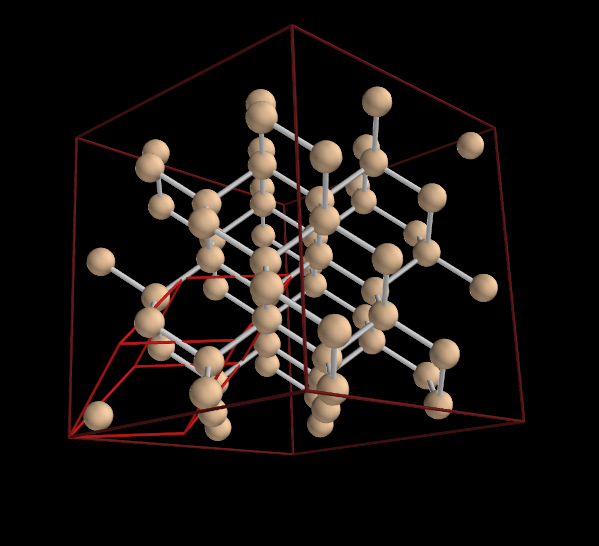
To visualize the tetrahedral structure of the silicon bonds we can use a larger cell, a so called super cell:
In [10]: s2=sc.supercell(2,2,2)
In [11]: v2=s2.vis()
In [12]: v2.pcell.show()
In [13]:
At the moment (April 2012) only a few crystal structures are built into gem directly. You can see a list with
In [6]: help(structures)
In general you start with an empty structure:
In [7]: s = Structure()
In [8]: print s
new structure
lattice constant = 1.0
lattice is incomplete.
0 atoms in unitcell
In [9]:
A lattice can be specified by adding three lattice vectors, which must form a right-handed system, and a lattice constant:
In [10]: s.add_lattice_vector([0.0,0.5,0.5])
In [11]: s.add_lattice_vector([0.5,0.0,0.5])
In [12]: s.add_lattice_vector([0.5,0.5,0.0])
In [13]: s.a0 = 5.4
In [14]: print s
new structure
lattice vector 0 = [ 0. 2.7 2.7]
lattice vector 1 = [ 2.7 0. 2.7]
lattice vector 2 = [ 2.7 2.7 0. ]
unitcell volume : 39.366 Ang^3
0 atoms in unitcell
In [15]:
Alternatively you can specify the Bravais lattice. The lattice of silicon is cubic ‘c’ and face-centered ‘F’: ‘cF’.
In [18]: s = Structure()
In [19]: s.lattice = Lattice(bravais='cF',a0=5.4)
In [20]: print s
new structure
lattice vector 0 = [ 0. 2.7 2.7]
lattice vector 1 = [ 2.7 0. 2.7]
lattice vector 2 = [ 2.7 2.7 0. ]
unitcell volume : 39.366 Ang^3
0 atoms in unitcell
In [21]:
Finally you add the atoms:
In [21]: s.add_atom(Atom('Si', [1/8,1/8,1/8]))
In [22]: s.add_atom(Atom('Si', [-1/8,-1/8,-1/8]))
In [23]: print s
new structure
lattice vector 0 = [ 0. 2.7 2.7]
lattice vector 1 = [ 2.7 0. 2.7]
lattice vector 2 = [ 2.7 2.7 0. ]
unitcell volume : 39.366 Ang^3
2 atoms in unitcell
atom 0 : Si [ 0.125 0.125 0.125]
atom 1 : Si [-0.125 -0.125 -0.125]
In [24]:
Export the structure in the flair input file format¶
In [12]: s.write_flair()
... writing to file inp using flair format.
In [13]: