![\begin{displaymath}
f(x) = \left\{ \begin{array}{lr}
(x+1) + (x + 1)^3& x\...
...]\\
4 + (x-1) + (x - 1)^3& x\in(0,1]
\end{array}\right.
\end{displaymath}](img1.png)
- Prove
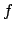 is a periodic function with periodicity of
is a periodic function with periodicity of 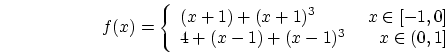 ;
;
- Find the trigonometric polynomial that interpolates
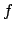 at
at
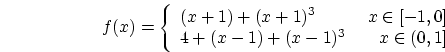 .
.
-
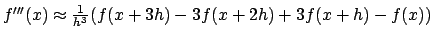 ;
;
-
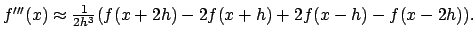
Part I: This part is the analytical part.
![\begin{displaymath}
f(x) = \left\{ \begin{array}{lr}
(x+1) + (x + 1)^3& x\...
...]\\
4 + (x-1) + (x - 1)^3& x\in(0,1]
\end{array}\right.
\end{displaymath}](img1.png)
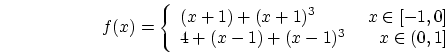 ;
;
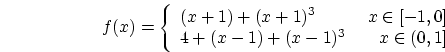 .
.
Part II: This part is practical
% hw7.m
% Implemention of the Richardson extrapolation algorithm
% on Page 510 of Kincaid&Cheney.
x = 3; h = 1; M = 6;
D = zeros(M,M); % Set D to be an M by M matrix with
% all zero entries
for n = 1 : M % In MATLAB, index has to start from 1
hn = h/2^(n-1); % Adapt the index in subsequent places
D(n,1) = ( log(x+hn) - log(x-hn) ) / (2*hn);
end
for k = 2 : M
for n = k : M
D(n,k) = D(n,k-1) + ( D(n,k-1) - D(n-1,k-1) ) / (4^(k-1) - 1 );
end
end
format long;
disp(D);