Matrix Pitfalls
Too many scientific programming problems arise from the improper use
of arrays on computers. This may be due to the extensive
use of matrices in scientific computing or the complexity of matrix
representations. In any case, here are some pitfalls to stay watch
for:
- Computers are finite
- Unless you are careful, you can run out of memory or run very slowly.
For example, let's say you store data in a four-dimensional array with each index
having a physical dimension of 100.
DIMENSION A(100,100,100,100)
or
double A[100][100][100][100];
This array occupies approx 1000 MB = ! GB of memory (if you even have that
much).
- Complex, Double Precision, Double Dimension
- Making a single precision matrix double precision, doubles the size of
the matrix. Making that matrix complex, doubles the size yet again.
Doubling the dimension of a matrix quadruples the size, and this makes
it real easy to run out of memory.
- Processing Time
- As a rule of thumb, matrix operations such as inversion requires
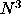 steps for a square matrix of dimension N.
Thus doubling the dimensions of a square matrix
(as happens when the number of integration steps are doubled)
leads to an eightfold increase in processing time.
steps for a square matrix of dimension N.
Thus doubling the dimensions of a square matrix
(as happens when the number of integration steps are doubled)
leads to an eightfold increase in processing time.
- Paging
- Many computer systems have virtual
memory in which disk space or some other slow memory is used
when a program runs out of RAM. The process of moving chunks of
memory are moved between the real RAM and the virtual memory is
called paging and it will slow down your computation
significantly.
If your program is near the memory limit at which paging occurs, a slight increase in the
physical dimensions of a matrix may require that the computer
has to use paging and lead to an order-of-magnitude
increase in running time.
- Matrix Storage
- The way arrays are stored in
memory differs between programming languages which becomes
crucial if you want translate a program into a different
programming language or use routines written in a different
languages as it is the case if you call a
LAPACK routine from within a C program
- Physical and Logical Dimensions
- When you run a program, you issue commands such as
double a[3][3];
or
DIMENSION a(3,3)
tell the computer how much memory it need set aside for
arrays. This is called physical memory} and is usually made
large enough to handle all foreseeable cases. Often you run programs
without the full complement of values declared in the dimension
statements (perhaps because you are running small test cases or
perhaps because you like to declare all dimensions to be 10000 to
impress your colleagues). The amount of memory you actually use to
store numbers is the matrix's logical size. For example, if you
declared
double a[3][3];
but only use a logical dimension of
[2][2]
then only four of the nine values of the matrix have been defined.
The rest might be zero or something or plain garbage.
Due to way arrays are stored in
memory the defined values do not occupy
sequential locations in memory and so an algorithm processing this
matrix has to know which values to pick out of memory. For this
reason, the subroutines you pull from a library often need to know
both the physical and logical sizes of your arrays.
Back to the LAPACK page.
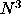 steps for a square matrix of dimension N.
Thus doubling the dimensions of a square matrix
(as happens when the number of integration steps are doubled)
leads to an eightfold increase in processing time.
steps for a square matrix of dimension N.
Thus doubling the dimensions of a square matrix
(as happens when the number of integration steps are doubled)
leads to an eightfold increase in processing time.